本节通过点对点信道模型的实验仿真，比较了对数和LMS算法（Log-Sum LMS，LOSLMS）与其他几种信道估计算法的性能。在第一个实验中，将信道冲激响应的长度设置为L=64，分别测试了64个系数中含4个非零值和6个非零值的情况，非零系数的值服从均值为零的高斯分布，且非零值在向量中的位置是随机的，信噪比分别设置为20 dB和30 d B。
测试算法包括ZA-LMS、RZA-LMS、加权l1-LMS、lp-LMS算法和LMS算法，lp-LMS算法的p值设置为0.5，将加权l1-LMS、lp-LMS算法的调节参数设置为ρ1=ρp=5×10-4，εp=ε1=0.05。ZA-LMS和RZA-LMS算法中的参数设置为ρZA=ρRZA=5×10-4，εRZA=10。所有算法的步长都设置为0.02。算法的均方误差曲线如图7-1~图7-3所示。
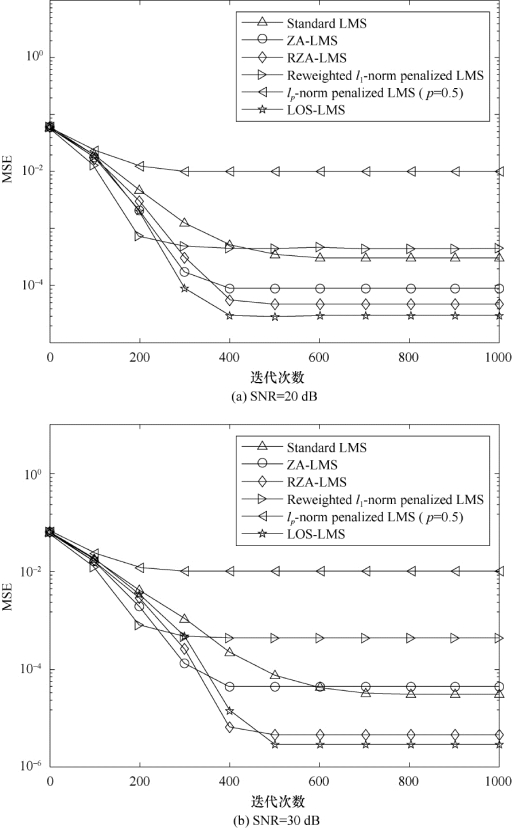
图7-1 算法的MSE曲线（稀疏度为4）
(www.xing528.com)
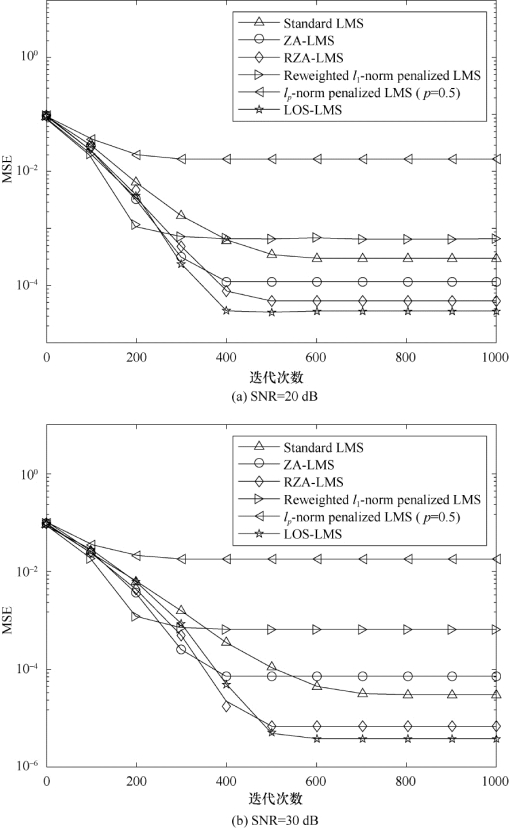
图7-2 算法的MSE曲线（稀疏度为6）
图7-1（a）和（b）为系统稀疏度为4时的仿真结果，图7-2（a）和（b）为系统稀疏度为6时的仿真结果。比较图7-1和图7-2发现，当非零系数个数增加时，算法的估计收敛性能将下降，在所有算法中，对数和约束的LMS算法性能普遍最优。
将信道冲激响应的长度设置为L=256，稀疏度设置为16，意味着系统冲激响应的系数包含有16个随机分布的非零抽头系数，抽头系数的值也服从均值为零、方差为1的高斯分布，仿真参数设置原则为使得所有算法达到最佳性能，ρp=5×10-6，ρ1=5×10-5，εp=0.05，ε1=0.01，ρZA=ρRZA=1×10-4和εRZA=10，信道比为30 d B。仿真结果如图7-3所示，观察曲线图，随着信道长度的增加，算法的稳态均方误差都有所改善，对数和LMS算法的收敛速度相比其他算法稍显不足，稳态收敛性能较其他算法较好。
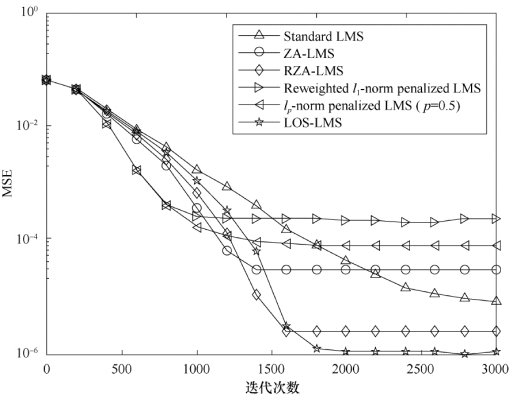
图7-3 算法的MSE曲线（信道长度为256，稀疏度为16，SNR=30 dB）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
