基于加权LMS算法的仿真实验分析：收敛性能与稳态性能对比分析

本节包括三个实验，以证明自适应滤波信道估计算法的性能。仿真中的测试算法包括标准LMS、ZA-LMS、RZA-LMS、加权l1-LMS算法以及l0-LMS算法，其代价函数和迭代更新表达式如表5-3所示。

表5-3　测试算法的基本公式

实验1 测试算法的收敛性能。假设协同中继系统中链路T1→R和R→T2的信道向量具有相同的长度Lg=Lk=16，则卷积级联信道的长度为L=Lg+Lk-1=31。分两种情况进行实验，第一种情况中，信道冲激响应g和k包含2个非零系数且均匀分布，其他系数均为零，使得系统的稀疏度为d=2；第二种情况中，g和k包含4个均匀分布的非零系数，其余系数均为零，稀疏度为d=4。

所有非零系数的值是从均值为零和方差为1的高斯分布中随机选取，将加权lp-LMS稀疏信道估计算法和加权l1-LMS算法的参数设置为ρp=ρ1=5×10-4，εp=ε1=1.2，在ZA-LMS算法和RZA-LMS算法中，参数设置为ρZA=ρRZA=5×10-4和εRZA=10。实验中所有算法的步长均为μ=0.02，算法分别在低信噪比（SNR）10 dB和高信噪比20 dB下迭代运行400次，实际信道状态信息和估计信道状态信息之间的均方误差曲线如图5-1和图5-2所示。

未知信道稀疏度为2时，算法的MSE曲线如图5-1（a）、（b）所示，稀疏度为4时的信道估计MSE结果如图5-2（a）、（b）所示。对比图5-1和图5-2，当信道的稀疏度增加时，也就是随着信道冲激响应中非零系数个数的增加，稀疏感知LMS算法的收敛性能将会降低。通过分析对比性能曲线，可知加权lp-LMS算法对未知系统的辨识性比其他算法都要好。在SNR=10 d B的情况下，l0范数约束稀疏滤波算法具有与加权lp-LMS算法相似的性能，由此可知，l0-LMS在低信噪比时可能具有较好的性能。

实验2 测试信道长度增加时，算法的收敛性能。系统中源节点—中继节点、中继节点—目的节点的链路信道向量具有相同的长度Lg=Lk=32，因此，卷积级联信道的长度为L=Lg+Lk-1=63。稀疏程度不同的情况有3种，在第一种情况下，信道冲激响应g和k中有两个非零抽头稀疏；在第二种情况下，信道冲激响应g和k包含4个非零的随机抽头系数；在第三种情况下，g和k包含16个非零的随机信道抽头稀疏。此三种情况中，非零抽头在信道系数向量中的位置均是随机选择的，非零抽头的值都服从高斯分布，未知系统的信噪比设为10 dB和20 dB，各算法的迭代步长μ取值同实验1，ρZA=ρRZA=5×10-4，εRZA=10，ρp=ρ1=5×10-4，且εp=ε1=1.2。

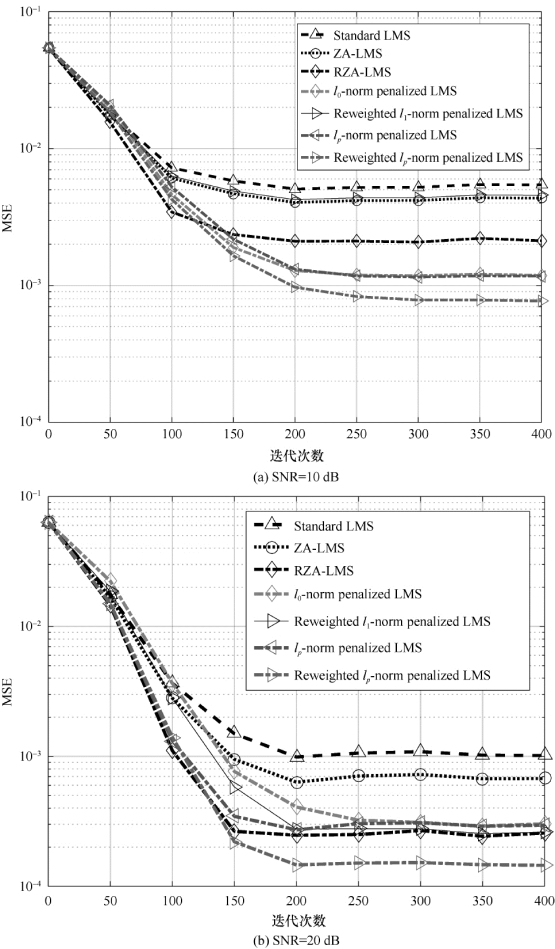
图5-1　算法的收敛与稳态性能（L=31，d=2）

注：Reweighted lp-norm LMS为加权lp-LMS算法，Reweighted l1-norm LMS为加权l1-LMS算法。

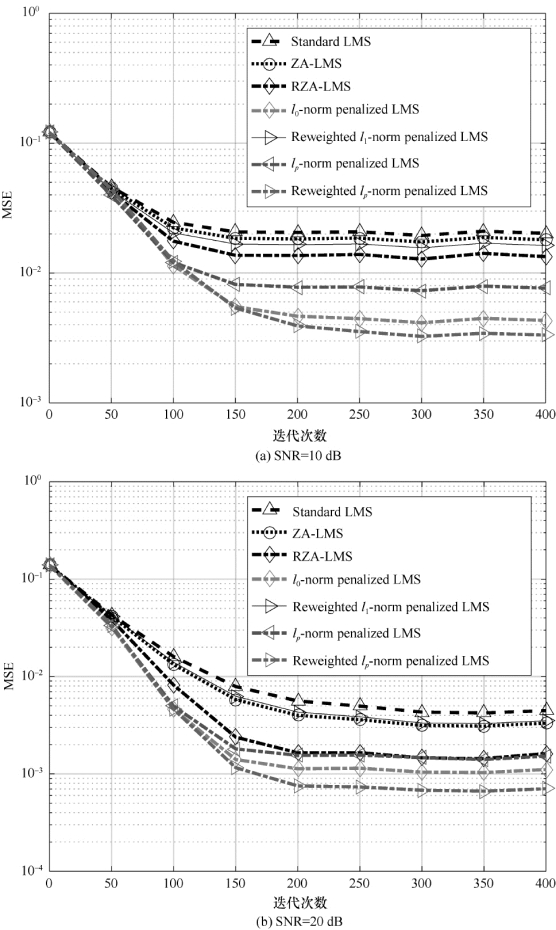
图5-2　算法的收敛与稳态性能（L=31，d=4）

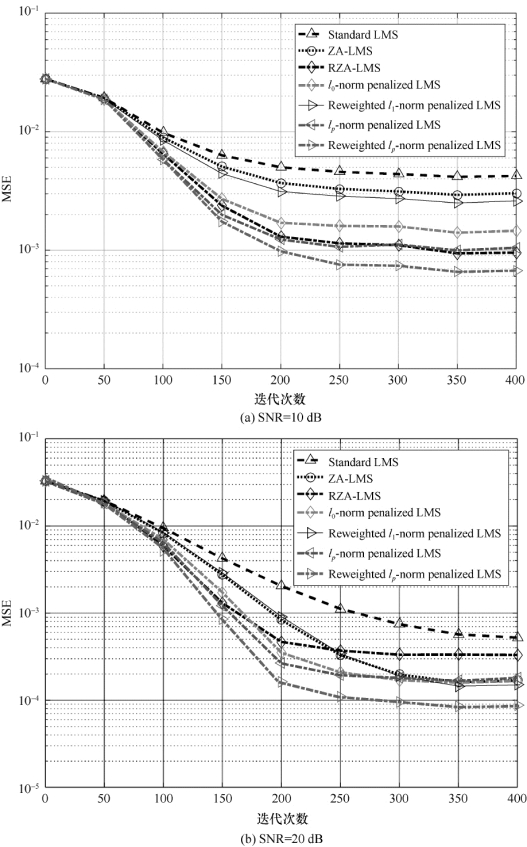
对比分析图5-3~图5-6所示性能曲线可知，低信噪比情况下，与其他算法相比，加权lp-LMS算法的稳态性能最好，收敛速度也更快。系统中非零个数相同的情况下，图5-3和图5-4的收敛性能优于图5-1和图5-2的收敛性能。理论推导表明，在相同的稀疏条件下，信道长度越长，信道估计的性能就越好，其潜在的因素是在该实验中系统具有较高的稀疏程度，将系统稀疏程度定义为d/L。

(www.xing528.com)

图5-3　算法的收敛与稳态性能（L=63，d=2）

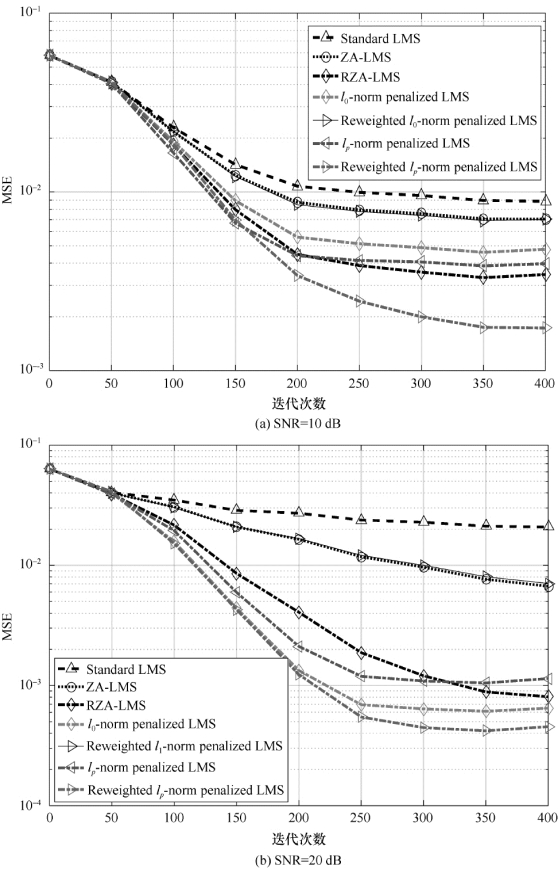
图5-4　算法的收敛与稳态性能（L=63，d=4）

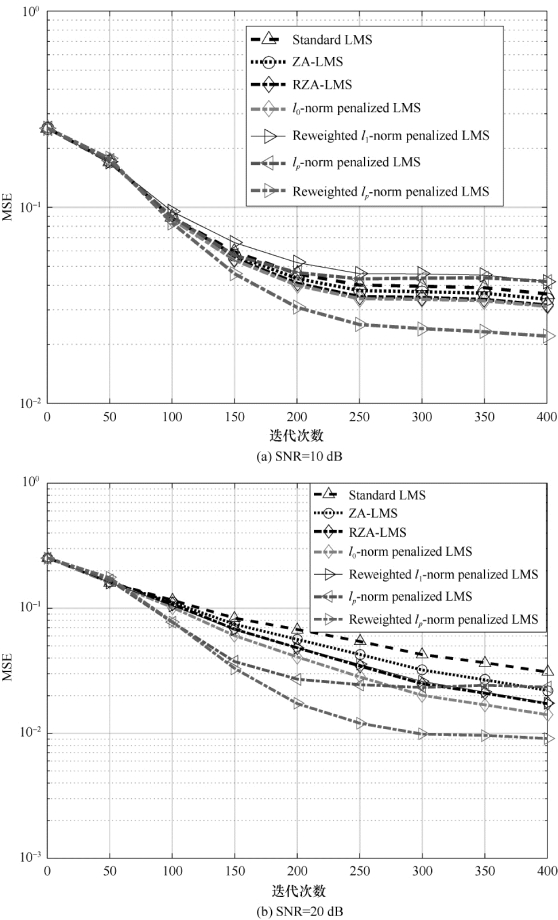
图5-5　算法的收敛与稳态性能（L=63，d=16）

实验3 稀疏度d、p值和L取不同值时，测试算法的收敛及稳态性能。分三种情况进行实验：（1）将稀疏度d设置为d=2/4/8/16，信道长度为Lg=Lk=32，测试加权lp-LMS及加权l1-LMS算法的性能；（2）加权lp-LMS算法中，lp范数的p的取值为p=0.4/0.5/0.7/0.9，稀疏度d=2，信道长度为Lg=Lk=32；（3）信道长度取不同的值，即Lg=Lk=16/32/64，稀疏度d=2。三种情况下，信道非零抽头的位置是随机选取的，仿真结果如图5-6~图5-8所示。

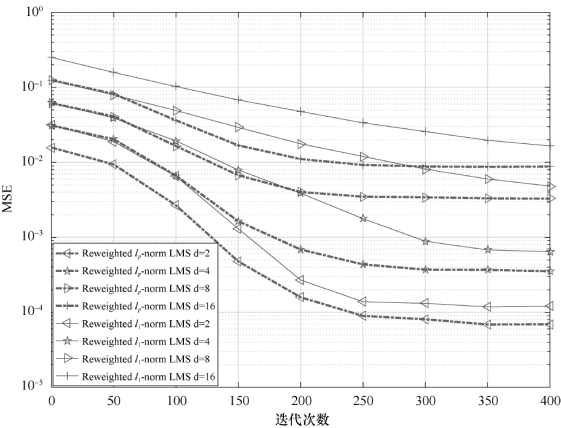
图5-6　稀疏度不同时，两种算法的收敛及稳态性能

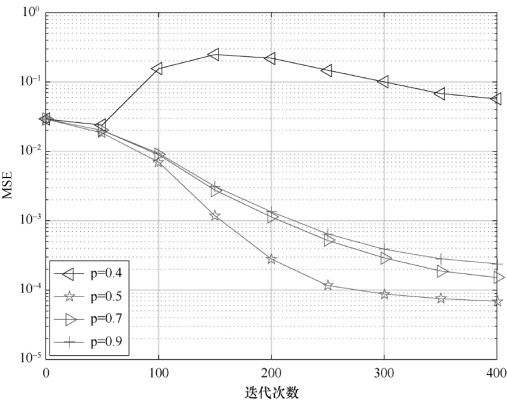
图5-7　取不同p值时加权lp-LMS算法的性能曲线

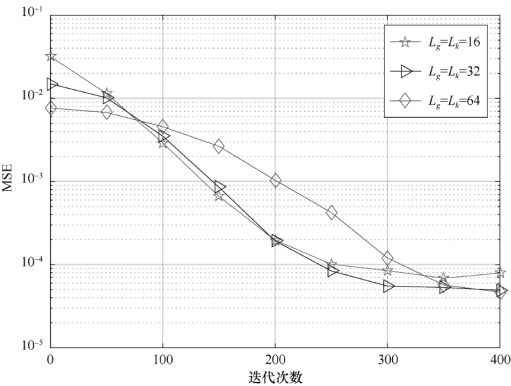
图5-8　信道长度不同时加权lp-LMS算法的性能曲线

当d的取值较大时，信道冲激响应将具有更多的非零系数，也就是说系统稀疏度较低。系统稀疏度变化时，加权lp-LMS算法和加权l1-LMS算法的收敛及稳态性能曲线如图5-6所示，分析曲线变化情况可知，两种稀疏感知LMS算法的性能随着信道稀疏度的增加而降低，其原因是式（5-15）中E[r∞]的值随着d的增加而增大。整体而言，加权lp范数惩罚的LMS算法比加权l1-LMS算法具有更好的估计性能。但在d值较大时，加权l1范数惩罚的LMS算法的收敛性能逐渐接近加权lp-LMS算法的性能。

分析图5-7所示的性能曲线，随着p（0<p<1）值的增加，加权lp-LMS算法的估计性能降低，由仿真结果可知，当p=0.5时，lp-LMS具有较好的估计精度。如图5-8所示，当系统信道长度由Lg=Lk=16增加为Lg=Lk=32时，也就是级联信道的长度从L=31变为L=63，加权lp-LMS算法的稳态性能更好，随着信道长度的持续增加，变化到Lg=Lk=64时，L=127算法的收敛速度逐渐减弱，随着迭代运行次数的增加，算法的稳态性能有所改善，此现象可以通过式（5-18）的稳态边界来证明。