稀疏度影响下的三种算法信道估计性能对比

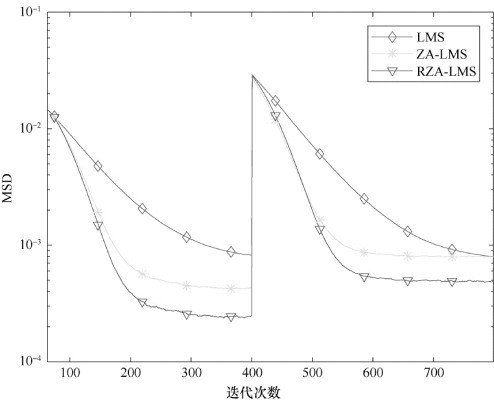
图4-2　SNR=10 dB时算法的跟踪情况对比

实验1 不同信噪比下算法的收敛性能和跟踪情况。参数设置情况为：PS=1，PR=1，μ=0.01，ρRZA=3×10-4，ε'RZA=0.3，SNR=10 d B/20 d B。信道的初始稀疏度设置为1，迭代400次后，信道冲激响应中非零系数的位置与大小皆发生跳变，信道的稀疏度变为4。算法独立运行100次，蒙特卡洛运行次数为1 000，信道估计的平均偏差曲线如图4-2和图4-3所示，其中，图4-2的信噪比环境为10 d B，图4-3的信噪比环境为20 dB。

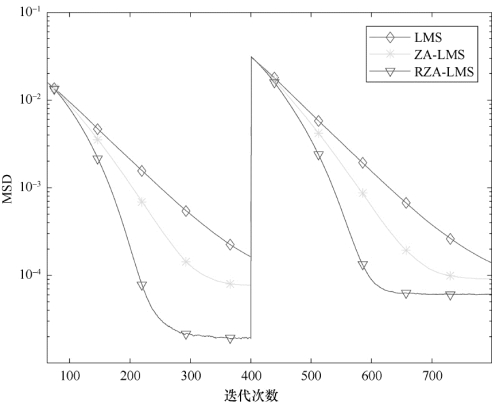
图4-3　SNR=20 dB时不同稀疏度的仿真性能对比

由图4-2和图4-3可知，在算法迭代的初始阶段，三种算法的性能较接近，RZA-LMS算法的收敛速度最快且稳态误差最小，ZA-LMS次之，LMS算法速度最慢、稳态误差最大。当信道状况发生改变，也就是系统的稀疏度由1变为4时，RZA-LMS和ZA-LMS算法很快能检测到系统的变化并根据新的稀疏度进行信道估计。由仿真结果可知，系统的稀疏程度越高，稀疏度感知算法的估计性能越好，稳态误差就越小；稀疏程度降低，标准LMS算法的稳态误差仅有细微变化，稀疏LMS算法的稳态误差增大，估计性能虽有所降低但是仍不低于标准LMS算法。实验1中各算法的稳态平均偏差数据如表4-1所示。

表4-1　实验1中各算法的稳态平均偏差

注：d为系统稀疏度。

对比图4-2和图4-3，并结合表4-1中的数据可知，图4-2的数据对应表4-1中SNR=10 dB栏，20 dB栏对应于图4-3的稳态平均偏差，随着系统信噪比的提高，各算法的估计性能都有所改善，RZA-LMS算法的改善幅度最大。由信噪比表达式SNR=10log（PS/PN），在训练信号的功率PS不变的情况下，当增加SNR时，噪声信号功率PN就会随之减小，算法的估计性能得到改善，稳态误差降低。(www.xing528.com)

实验2 加权零吸引算子ε'RZA的取值分析。本实验中的参数分别设置为：ε'RZA=0.3/0.1，SNR=10 d B，μ=0.012。当改变ε'RZA值时，RZA-LMS算法的估计性能随之改变，仿真结果如图4-4和图4-5所示，相应的稳态平均偏差数据如表4-2所示，其中，ε'RZA=0.3时的仿真结果对应于图4-4中各算法的稳态偏差值，ε'RZA=0.1时的数值是图4-5中各算法的稳态偏差值。

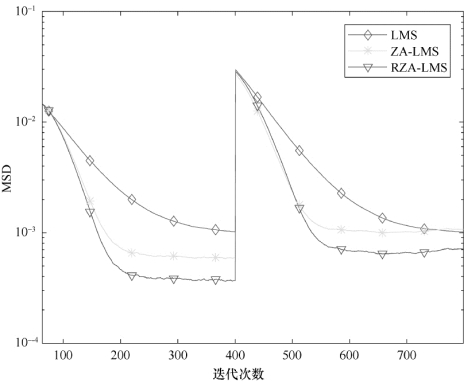
图4-4　ε'RZA=0.3时不同稀疏度的仿真性能对比

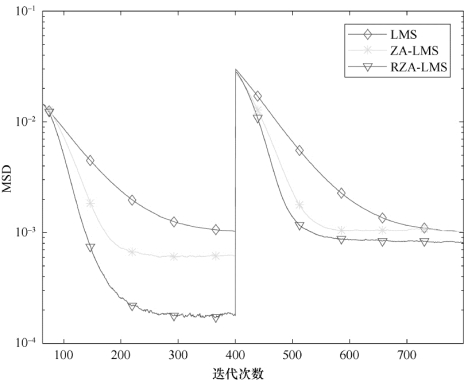
图4-5　ε'RZA=0.1时不同稀疏度的仿真性能对比

对比图4-4和图4-5可知，ε'RZA=0时，RZA-LMS算法的信道估计性能较好，对于稀疏信道，加权零吸引算法能有效挖掘幅度接近于ε'RZA的抽头系数，将幅度小于ε'RZA的抽头系数趋于0。当ε'RZA取值很小时，该算子控制模型式（4-11）更接近于l0范数，当|hi（n）|≫ε'RZA时，收缩能力会减弱。因此，适当选取ε'RZA的值将有助于减小RZA-LMS算法的稳态误差。

表4-2　实验2中各算法的稳态平均偏差

注：d为系统稀疏度。

另外，对比表4-1和表4-2的稳态偏差数据，在ε'RZA=0.3时，与实验1相比，实验2仅μ值增大，其余仿真参数未变，表4-2中的结果均大于表4-1中的数值，当增大梯度下降步长时，系统的收敛速度加快，系统误差能快速达到稳态，但稳态误差将会增大；当减小梯度下降步长时，系统的稳态误差将会降低，但系统的收敛速度变慢。