本节给出SAEM算法和CoSa MP算法以及OMP算法的估计性能比较,后两种算法是在稀疏度已知的情况下进行信道重构。实验是在MIMO中继多径时变信道环境下进行的,天线数目为MS=MR=MD=2。随机产生104个符号,采用QPSK调制,训练序列的长度为100,数据块的长度为1 200。每条链路中每30个抽样里面设置6个非零值,其他全部为零。每个数据块内稀疏度不变,数据块外是变化的。信道模型采用AR模型,并用卡尔曼滤波对参数进行平滑处理。仿真中所采用的时变多径信道根据Jake模型产生。多普勒频移为0.002,信道估计的均方误差与信噪比的关系如图3-5和图3-6所示。
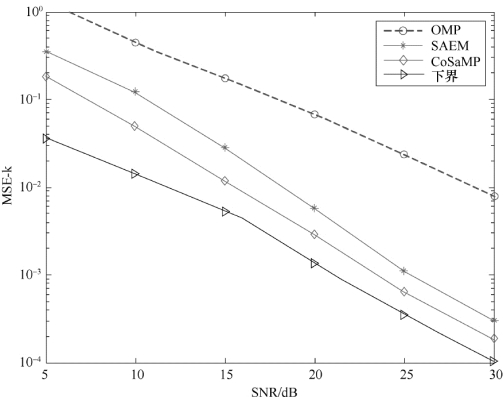
图3-5 SAEM算法与CoSaMP算法的性能比较

图3-6 增加迭代长度后SAEM算法的估计性能
仿真结果表明,由于该算法引入了平滑思想,在稀疏度未知的情况下,能够较为准确地估计出信道参数,说明所提方法能够较为准确地探测到信道的稀疏结构,作为稀疏度自适应的SAEM算法的估计性能,相比CoSa MP算法稍差,但是比OMP算法更接近性能下界,这是因为OMP算法在高维信号空间并不是稳健的。图3-6显示,进一步增加算法的迭代次数后,估计性能的效果更佳,逐渐逼近信道估计下界的性能。
图3-7和图3-8给出了当协同信道中非零抽头数目改变时的仿真结果,从仿真图的曲线可知,平均MSE性能随着信噪比的增加而提高。为了验证算法的有效性,本节基于式(3-10)所代表的信道模型,提供了基于压缩感知算法、基于期望条件最大化算法仿真性能的对比,如图3-9所示,由性能曲线可知,基于CS算法的估计性能优于线性算法,并很好地接近系统性能下界,CoSa MP算法的性能也优于OMP算法。

图3-7 系统稀疏度为2时信道估计算法的性能(https://www.xing528.com)
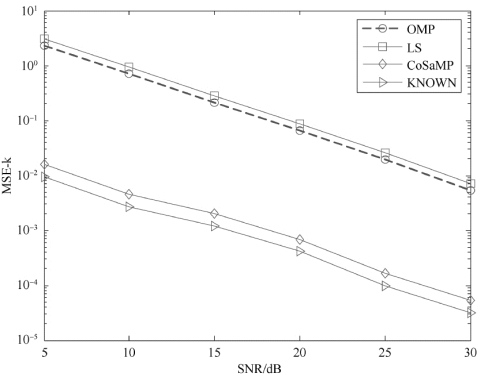
图3-8 系统稀疏度为4时信道估计算法的性能

图3-9 CoSa MP压缩感知算法与期望条件最大化算法的性能比较
由图3-7和图3-8可知,随着信噪比的增加,信道估计的性能也在增加。图3-7和图3-8是在稀疏度不同时的仿真结果,图3-7的系统稀疏度小于图3-8,当系统稀疏度较小时,基于压缩感知算法的估计性能较好。如果在稀疏度相同的情况下,增加训练序列的长度,估计性能也会改善。
如图3-10所示,在时变信道中,所提出的稀疏度自适应期望最大化算法的估计性能接近下界,这意味着SAEM信道估计器能够以相当好的精度检测稀疏结构。
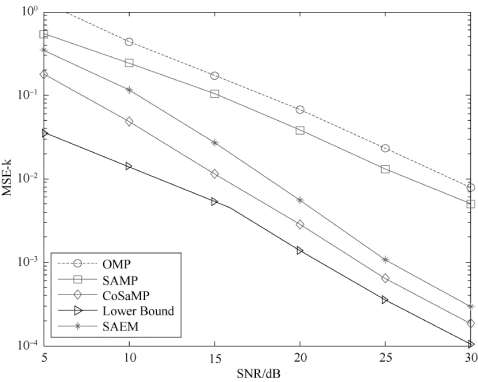
图3-10 SAEM与其他算法的性能对比
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




