MIMO协同单向中继系统稀疏信道估计优化

本节主要探讨放大转发协议下多天线中继协同系统的稀疏信道问题。首先，介绍单向MIMO中继网络的系统模型，并将复合信道估计表示为基于稀疏正交分解理论的压缩感知问题；然后，用压缩采样匹配追踪算法重构复合信道；最后，进行计算机仿真并与传统方法进行对比，以验证所提方法的有效性。由于MIMO协同信道不同于MIMO系统的信道情况，前者是多个信道的卷积形成的信道矩阵，信道矩阵的维数相应大幅增加，给信道估计带来了计算上的复杂性，另外，Bajwa曾证明信号在高维空间表现出更加稀疏的特点，基于该观点，结合矩阵的分解理论，可应用压缩感知理论对MIMO协同中继信道进行估计。本节的贡献在于首次提出MIMO中继网络中基于压缩感知的稀疏信道估计技术，对有效挖掘MIMO中继协同信道的稀疏特性有重要意义。

放大转发协议中，典型的MIMO协同中继系统模型如图3-3所示。系统由源节点MS、中继RS和目的节点BS组成。源节点通过中继节点的帮助向目的节点发送信息。假设源节点有MS个天线，中继节点有MR个天线，目的节点有MD个天线，假设系统中所有的信道为准静态频率选择性信道。本节讨论MS到BS之间级联信道的估计问题，也就是系统上行链路的信道估计。

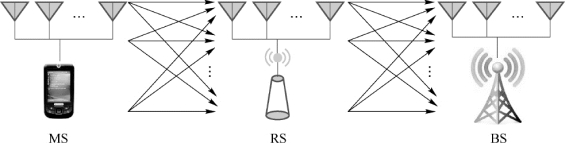
图3-3　MIMO协同中继系统模型

定义源节点的第l根天线与中继节点的第r根天线之间的信道冲激响应为

其中，L1表示源节点与中继节点之间的信道长度，hr，l是复高斯随机变量，其均值为零，方差为δ21。同样，定义目的节点的第m根天线与中继节点的第r根天线之间的信道冲激响应为

信道冲激响应服从复高斯分布，其均值为零，方差为δ22，L2代表目的节点与源节点之间的信道长度。考虑到源节点与目的节点之间的远距离以及信道损失问题，假设源节点与目的节点之间的MS-BS链路不存在。本节所有的信道估计问题是在系统完全同步假设的基础上开展的。

在第一时隙，源节点向中继节点发送信号，MS节点第l根天线的发送信号表示为xl=[x（0），x（1），…x（N-1）]T，为了减少块间干扰，发送之前在发送信号中插入循环间隔，循环间隔的长度为LP，LP≥max（L1-1，L2-1）。中继RS接收到信号后，去除循环间隔，接收信号如式（3-1）所示：

其中，信道矩阵H、发送信号x及接收信号yR可分别表示为

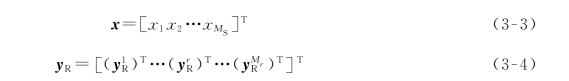
矩阵Hr，l是N×N的循环矩阵，其第一列元素的形式为

(www.xing528.com)

n1是MR×1维的零均值高斯噪声序列。

其中，

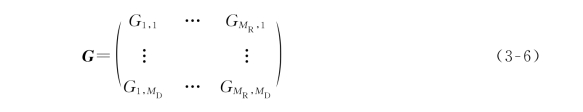
矩阵Gr，m是N×N的循环矩阵，其第一列元素的形式为

其中，

因此，βGr，m Hr，l可以表示为

式（3-7）中循环矩阵的第一列为[β（gr，m*hr，l）01×（N-L+1）]T，定义复合信道kl，m=[kl，m（0），kl，m（1），…，kl，m（L-1）]，L=L1+L2-1，可以得出下列公式：

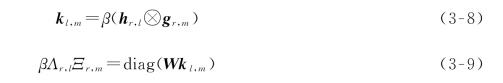
对接收信号yD进行DFT变换，系统模型可以表示为

其中：X=diag（Fx）W；F是离散傅里叶变换矩阵；W是由矩阵 N F的前2L-1列元素组成的矩阵；n=（I⊗F）n3。