基于凸分析的稀疏正则化算法优化

线性方程组的稀疏近似解是基于l1范数正则化的经典最小二乘法，但这种方法往往低估了真实解。作为l1范数的一种替代，Ivan Selesnick提出了一类非凸罚函数，使最小二乘代价函数的凸性最小，避免了l1范数正则化的系统低估特性。该惩罚函数是极大极小凹罚的多元推广，是根据Huber函数的一个新的多元推广定义的，而Huber函数又是通过精细卷积来定义的。通常情况下，信号重建建立在稀疏近似的基础上。线性方程组y=Ax的稀疏近似解可以通过凸优化方式获取，常用的解决方法是使正则化的线性最小二乘代价函数最小化，代价函数J：R N→R为

其中，l1范数是经典的正则化项，因为在凸正则化项中，l1范数能够最有效地诱导稀疏性。但是，当x∈R N时，式（2-16）通常会低估其中的高幅值分量。非凸稀疏性诱导正则化已被广泛使用，对于高幅值的分量能够获取更精确的估计值，在非凸优化中，其代价函数一般是非凸的，并且具有外部次优、局部极小值。

基于稀疏正则化线性最小二乘的非凸罚函数，推广了l1范数，使最小二乘代价函数的凸性最小。假设F：R N→R，含非凸正则项的代价函数为

其中，ψB：R N→R为非凸惩罚项，该项可使得代价函数F保持凸性。惩罚项ψB由矩阵B参数化设置，F的凸性依赖于矩阵B的合理设定，而矩阵B的选择取决于矩阵A。线性算子矩阵A可以是任意的，与l1范数相反，该非凸方法不会系统化低估高幅值分量的稀疏向量。同时，由于式（2-17）是凸的，所以代价函数不具有次优局部最小值。

利用凸分析工具定义一类新的非凸惩罚。特别是，利用非正式卷积定义一个新的多元概括的Huber函数。反过来，利用广义Huber函数定义了非凸惩罚项，使得代价函数的凸度最小。

由Huber函数（如图2-4所示）的定义：Huber函数s：R→R定义为

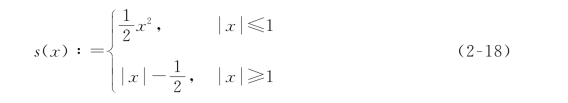
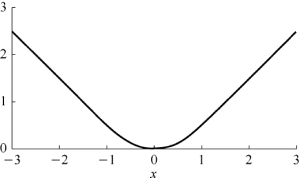
图2-4　Huber函数

Huber函数可以写成(www.xing528.com)

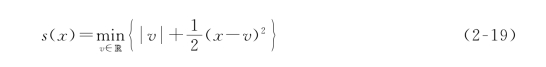
Huber函数是Moreau包络的一个标准例子，此处记为，给定x∈R，v=0，x-1，x+1时，式（2-19）存在最小值。

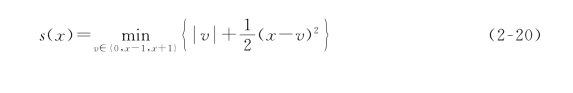
因此，Huber函数可以表示为

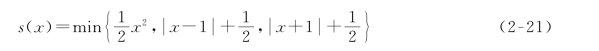
极小极大凹（MC）罚函数φ：R→R（如图2-5所示）定义为

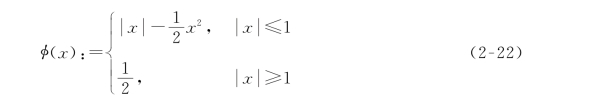
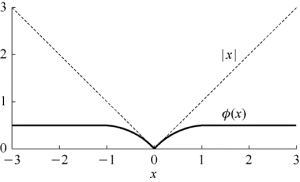
图2-5　极小极大凹惩罚函数

极小极大惩罚项可以表示为

其中，s是Huber函数。最小最大惩罚项的表示将具有较好的稀疏表示作用。