稀疏重建算法：基追踪、凸松弛与压缩感知

压缩感知理论的思想是将传统的信号采样步骤与压缩步骤合并，通过已知的非线性测量矩阵与观测得到的信号，利用有效的稀疏重建算法准确重建原始稀疏信号。稀疏信号的重建算法是压缩感知的核心理论之一，从数学理论上看，零范数最优化算法可以获得最优稀疏解。但是，零范数最优化算法是一个（Nondeterministic Polynomial-time，NP）难题，也就是说求解这种零范数最优化解是一个不确定性问题。

斯坦福大学的David Donoho教授从理论上证明，如果测量矩阵满足互不相干特性，利用凸松弛算法可以近似求解零范数最优化算法并得到次优解（Suboptimal Solution）。斯坦福大学的Emmanuel Candes教授从随机测量矩阵的严格等距特性出发，证明如果测量矩阵满足RIP，则凸松弛算法也可以近似求解零范数最优化非确定性多项式难题。基追踪（Basis Pursuit，BP）算法、最小绝对值收缩和选择算子（Least Absolute Shrinkage and Selection Operator，Lasso）算法、基于lq范数的最优化算法、Dantzig选择（Dantzig Selector，DS）算法、迭代重加权l1范数最小化算法、梯度映射稀疏重构算法都属于凸松弛算法。其中，根据算子范数的不同，BP、Lasso和DS算法有时候统称为混合范数算法。

与传统线性信号重建算法相比，凸松弛算法的计算要复杂得多。主要是因为凸松弛算法需要转化为线性规划来求解。另外，在实际信号处理系统中，凸松弛算法实现起来也非常困难。所以，在信号处理领域，有必要发展计算复杂度低的稀疏重建算法。随着压缩感知理论的发展，涌现出了很多复杂度较低的稀疏重建算法，如贪婪算法、凸优化算法以及其他算法等。业界对贪婪算法的研究比较深入，分类也更详细。凸优化算法主要包括基追踪算法，基于l1范数的基追踪算法、梯度投影（Gradient Projection of Sparse Reconstruction，GPSR）算法等。

1.凸优化算法

由于采用精确的l0范数求稀疏解非常困难，并且效率不高，因此此类问题通常转化为以下凸松弛问题：

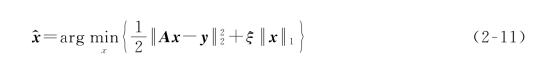
l1范数广泛应用于求稀疏解的算法，尤其用于基追踪算法中。

l1范数逼近l0范数的理论分析：从几何学的角度，可以分析说明在二维欧几里得空间，l1范数逼近l0范数的原理。

图2-2中的直线y=Ax可表示为系统中所有满足最稀疏特性解的集合。图2-2（a）中，l2范数是一个圆形，它的最外侧边界和直线的交点能够落在坐标轴上的概率几乎为零，除非直线的斜率为无穷大或者是零，而直线的斜率为无穷大或者零的情况是不存在的，所以l2范数解并不是问题的最稀疏解。图2-2（b）中l1范数是一个菱形，它的四个角都在坐标轴上，该图形从无限小逐渐变大的过程中最先和直线相交的点出现在坐标轴上。从图中可以看出只有一个点落在y轴上，也就是只有一个非零值，l1范数满足约束条件的最稀疏解。

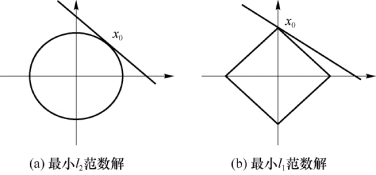
图2-2　最小范数解示意图

最初，基追踪算法仅适用于无噪测量值求解的情况，而基追踪降噪算法用于有噪矢量的情况，这两种算法统称为基追踪算法。另外，Lasso算法在统计学中很受欢迎，在合适的参数配置下，该算法可以与BP算法表现出相同的性能。

以上算法的共同之处在于将非凸问题转化成凸优化问题求解信号的逼近值，可以通过内点法、投影梯度法和迭代阈值法等先进方法求解。由于松弛和数值的精度，求出的解可能不是严格稀疏的，但解中会有很多对估计误差影响甚微的值。如果希望得到严格稀疏的解，需要另外设置阈值或者经过一个去偏置的过程以去除解中的甚小值。

2.贪婪追踪算法

另外一种解决组合问题的方法是基于动态规划的方法，即贪婪追踪算法。该方法的思路是，算法每次迭代时都要选择一个局部最优解，通过每次的局部最优以达到逐渐逼近原始信号的目的。贪婪追踪算法主要包括匹配追踪（Matching Pursuit，MP）算法以及正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法等。

贪婪追踪算法由于具有易于实现、计算复杂度低等特点而广受欢迎。近年来，通过加强一些约束关系，该算法能够得到最优解，促使大家对动态规划方案产生新的兴趣，从而促使更新、更优贪婪算法的产生。(www.xing528.com)

3.lq（0<q<1）最优化算法

由压缩感知观测值利用lq最优化算法重构信号的问题主要是解决三类最小值问题之一。

（1）由稀疏集约束lq优化最小值问题，可描述为

（2）基于l2范数误差约束的lq优化最小值问题，可描述为

（3）松弛情况下的描述：

其中，ρ是调节因子。图2-3所示为lq范数最小化方法，当q≥1时，以上三种最小化问题均为凸优化问题，并且可以互相替换。当0<q<1时，以上问题转换为非凸优化问题，采用相关算法解决。

图2-3　lq范数最小化方法

4.其他算法

基于压缩感知理论的重建算法还包括迭代门限算法，与贪婪追踪算法非常相近。迭代门限算法主要包括以下几种算法：压缩采样匹配追踪（Compressive Sampling Matching Pursuit，CoSa MP）算法、迭代硬门限（Iterative Hard Thresholding，IHT）算法、子空间追踪（Subspace Pursuit，SP）算法、迭代软门限算法（IST）、两步门限近似信息传递（TST-AMP）算法以及加速硬门限（Accelerated Hard Thresholding，AHT）算法。在提出的诸多门限算法中，迭代硬门限是最简单的算法，寻找信号y的d稀疏表示信号x，可以通过下面的迭代过程实现：

其中，Hd（a）表示非线性运算子，它将a中除最大d元素以外的所有元素均设置为零。