振动分析及特征参数提取方法

振动分析就是将测量获得的振动信号中含有的与设备状态有关的特征参数提取出来。根据振动分析信号处理方式的不同,分为幅域分析、时域分析和频域分析。 不同的振动信号分析方法可从不同的角度观察、分析信号,从而可根据不同需要得出各种信号处理结果。 这里仅介绍一种幅域分析方法。

信号幅域分析是在波形的幅值上进行的,如计算波形的最大值、最小值、平均值、有效值等,它也研究波形幅值的概率分布问题。 信号的幅值是从总体上反映信号强弱的特征参数。在幅域分析中,对波形幅值的研究通过以下几个参数进行。

(1）峰值Xp

峰值是表示振幅的单峰值。 在实际振动波形中,单峰值表示瞬时冲击的最大幅值。 Xp﹣p表示振幅的双峰值,又称峰-峰值,它反映了振动波形的最大偏移量。

(2）平均值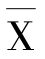

平均值是表示振幅的平均值,是在时间T 范围内设备振动的平均水平。 其表达式为

(3）有效值Xrms(均方根值）

有效值Xrms表示振幅的有效值,它表征了振动的破坏能力,是衡量振动能量大小的量。ISO 标准规定,振动速度的均方根值(即有效值)为“振动烈度”,作为衡量振动强度的一个标准。 有效值的数学表达式为

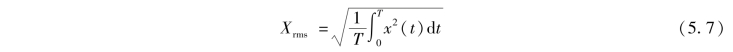
幅域分析法中,对波形幅值概率分布的研究是通过概率密度函数进行的。 概率密度函数是表示信号幅值落在指定区间内的概率,它提供了关于振动信号的两个信息:一是信号幅值落在指定区间内的概率,二是信号沿幅值域分布的信息。 例如,对于如图5.3(a)所示的信号,x(t)值落入(x,x ﹢Δx)区间内的时间为Tx,即

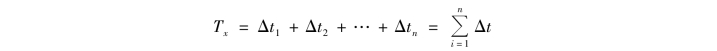(www.xing528.com)

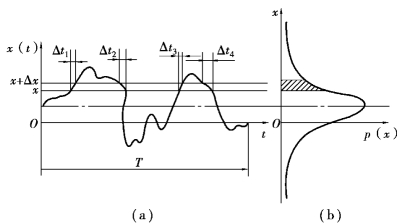
图5.3　概率密度函数的计算

当样本记录的观察时间T 趋于无穷大时,Tx/T 的比值就是幅值落在(x,x ﹢Δx)区间内的概率,即

定义幅值概率密度函数p(x)为

如图5.3(b)所示为信号沿幅值域分布的情况,坐标x 表示信号x(t)值的大小,而阴影部分的面积则表示信号x(t)的值落在(x,x ﹢Δx)区间内的概率。 概率密度函数曲线与x 轴所包围的面积是“1”。 不同信号有不同的概率密度函数图形,可以借此识别信号的性质。 图5.4所示为常见的四种信号的概率密度函数图形。

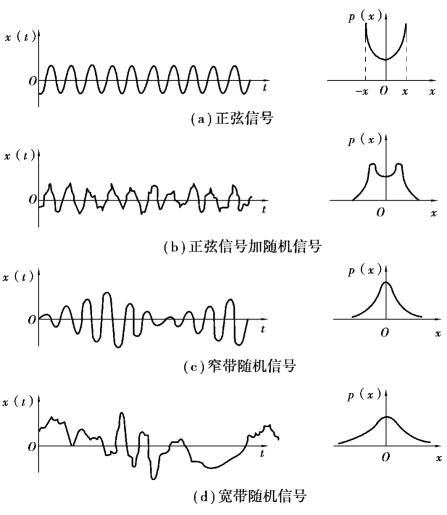
图5.4　常见的四种信号的概率密度函数

概率密度函数可以直接用于机电设备的故障诊断。 图5.5 反映车床变速箱噪声的分布规律,可以看出,新旧两台变速箱的分布规律有明显的差异。 新车床的概率密度函数图形呈“窄而高”的形态,而旧车床的图形呈“宽而矮”的形态。 显然,旧机床噪声的幅值大于新车床的幅值。

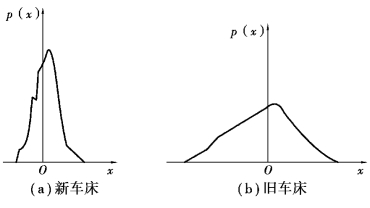
图5.5　车床变速箱噪声的概率密度函数