线性反馈系统的设计与优化

对于线性系统来说，稳定性和输入-状态稳定性问题可以用代数方法解决，有很多有效的计算工具可以利用。

让我们回顾如图5-8所示，实际上是如图7-4中所示线性系统的一个特殊情况。可以有助于理解反馈可以改变系统稳定性，反馈回路可以使得回路中两个不稳定的系统获得稳定的状态。令前向通道从u₁到y₁的表达式为G₁（z）=N₁（z）/D₁（z）。反馈机构从u₂到y₂的表达式为G₂（z）=N₂（z）/D₂（z）（此处为负反馈，见5.6.2节）。用框图表示，我们很容易得到u到y=y₁的表达式：

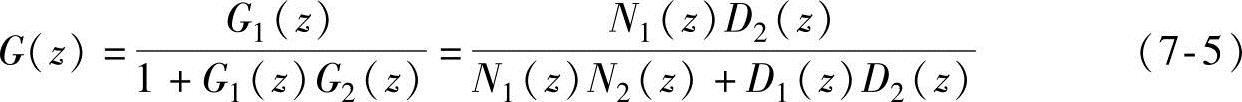
分母N₁（z）N₂（z）+D₁（z）D₂（z）=0的方程根显然与D₁和D₂的根不同。也就是说，子系统G₁和G₂的稳定性不能代表整个反馈系统的稳定性。而反馈系统的稳定性也不能代表子系统的稳定性^[5]。

举例来说，我们将G₁看成是连续时间的一个纯积分器，G₁（s）=1/s，反馈系统的增益为一个纯标量G₂=g₂/1。基于上面的计算结果，闭环稳定性是由g₂+s决定的，所以当g₂>0时，反馈系统稳定（详见式6-7附近内容的分析）。开环系统G₁不稳定。积分器的增益裕度是无穷的。在G₂中应用一个负的增益可以得到正反馈的效果，这使得系统发散。

相似地，在离散时间情况下，G₁（z）=1/（z-1），积分器也是在离散时间条件下使用的，反馈系统G₂=g₂是一个标量。当g₂+（z-1）=0的根小于1时，反馈回路是稳定的，唯一的根为1-g₂。也就是当g₂∈（0，2）时，开环系统也是不稳定的。增益裕度是有界的，值为2。负的增益或者是大于2的增益都会使得系统不稳定（参考6.4.3节的例子）。

使用波特图和奈奎斯特图，可以检查回路增益G₁G₂来确定系统稳定的边界条件，这也解释了在计算机出现之前频率法的流行。绘图方法是一个强有力的设计工具。频率法的关键是要保证回路增益G₁G₂的幅值永远不能大于1，相位角偏移不能超过180°。

运用频率法，可以得到5.7节中描述的一个或者两个积分器的不稳定性需要用正反馈。

如图5-14所示的只有一个积分器的回路中，结论是显而易见的，我们可以采用正反馈来得到无界响应（在上面刚进行过分析）。运用频率法的思想，将正弦波信号作为输入，显然积分器可以产生一个频率相同的正弦波输出，但是相位移等于-π/2^[6]，与频率无关。回路增益可以任意大，也不会发生不稳定的情况。(www.xing528.com)

即使我们用了负反馈控制也可能在回路中产生正反馈。正如前文讨论过的，回路中的元素决定了回路增益和相位移动。假设对于某些频率相位移动为φ=-π弧度或-180°。这意味着符号发生改变，如果这一频率下的增益大于1，作用效果就接近于正反馈，闭环回路不稳定。如果增益恰好为1，则发生等幅振荡。

这一现象可以解释回路不稳定性，并且可以作为伯德图法与奈奎斯特图法的稳定性条件。

如图2-13所示，不考虑摩擦力时，系统具有两个积分器，相位偏移-180°。每个积分器分别产生了-90°的相位偏移，因此总的相位偏移φ=-180°。回路增益值为1/ω²，于是当ω=1时，回路增益为1（通过这种方式可以识别共振模式）。

对于3个积分器串联的情况，任何常值反馈系统都将变成不稳定的系统。为了举例说明反馈的作用，我们用一点小的技巧。首先，我们用一些小的负反馈回路包围每一个积分器，以便在前向通路可以得到良好的稳定性能。如图7-5所示，每个系统的相位偏移从0°～90°不等。因此，整个系统的相位偏移从低频的0°～高频的270°。（由两个线性系统串联连接成的线性系统的相位偏移是每个线性系统相位偏移的和。）

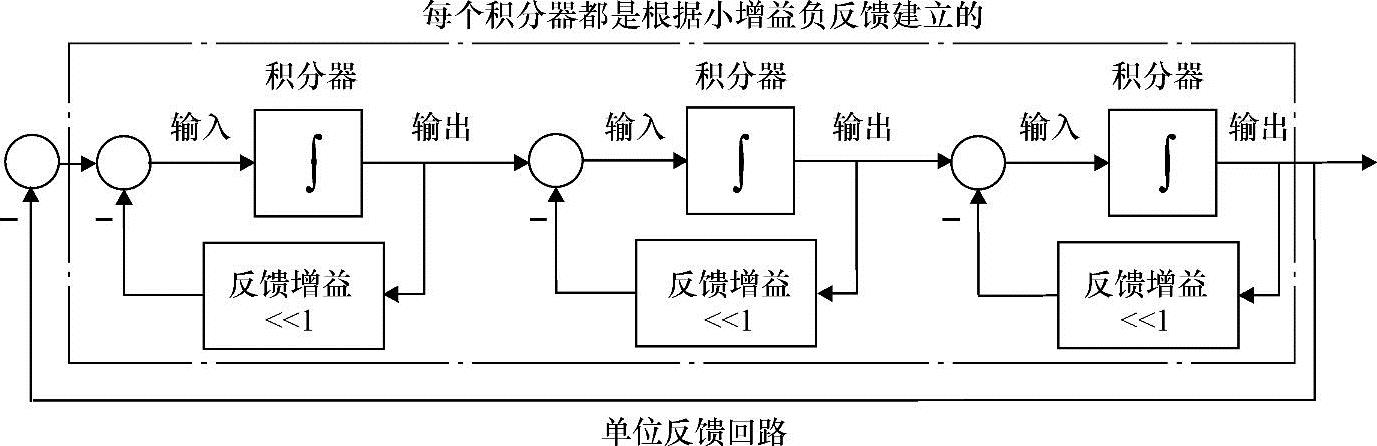
图7-5 3个连续稳定反馈积分器，单位反馈，小增益下不稳定

假设含有3个积分器的系统采用单位反馈。回路中内部元件的反馈增益越小，整个前向通道的增益越大。假如引入的反馈增益充分小，这说明在相位偏移180°时的回路增益大于1，最终会导致整个系统不稳定。