如何提高7.4系统的稳定性和调节策略？

正像我们在前面章节讨论过的那样，反馈具有使一个不稳定系统稳定的能力。这也意味着反馈可以使一个稳定系统变得不稳定。如在6.4.3节讨论过的例子，α是可调节的反馈参数，系统的响应可以被调节（稳定、不稳定、振荡和阻尼）。如果α在区间{0，-2}外，系统将不稳定，因此只有很小的区间可以使系统稳定。

在一个更接近实际的物理环境下，例如一个典型的伺服电动机应用，伺服电动机的轴需要固定在特定的角度（如广播天线需要固定方向的例子），如图7-3所示。

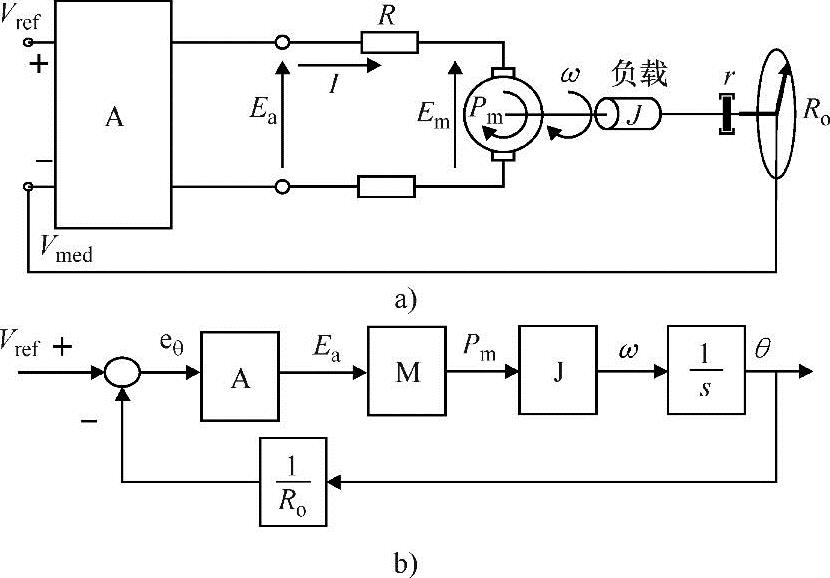
图7-3 直流伺服电动机

系统变量在图7-3中已经标注出来了。整个系统包括功率放大器/整流器、机械惯量、电动机轴上的摩擦力矩以及在电动机速度与电动机角位移两端连接着的积分器。在前向通路在Ea和位移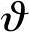之间包含有积分器。由于积分器的存在，任何给定的固定角位移都是开环不稳定的。如果施加一个电压，那么电动机将会转动，轴也会一直旋转，系统是不稳定的。(www.xing528.com)

因此需要引入负反馈以产生驱动电压。例如图7-3a所示的放大器带有两个输入，正极端子的电压与所需的位置成比例；负极端子的电压与当前的轴位置成正比。如图7-3b所示，只要在两个输入之间存在误差或差异，放大器就会产生电压，电动机就会起动，向正确的方向旋转，进而减小误差（负反馈）。当误差消失时，电动机两端电压就会消失，电动机停止转动。

如果放大器增益过高，电动机转动惯量的存在将会引发一个棘手的问题。只要电动机接受驱动电压，就会产生转矩并旋转，在增益很大的情况下，即使位置误差非常小，这个驱动电压也会非常大，电动机将会以非常大的转动惯量使其停止或反转。当驱动电压改变了极性，最后电动机也会反转。整个循环的过程中，产生了我们不想要的波动。反馈的运用也需谨慎。

可以观察到，为了实施反馈，需要额外的系统部件：需要建立反馈通路的元件。在这个伺服电动机的例子中，传感器可以只是一个简单的电位计，将轴向位置转换为电压信号。在其他的应用中，可能会由于找不到恰当的检测装置影响反馈的应用。

尽管伺服电动机的物理构造与马桶的水箱截然不同，但是两者的响应特性确实是相同的。主要的特性都是积分器（电动机或马桶水箱）和带有增益元件（放大器或浮子）的负反馈。将它们放在一起就会产生一个恒定的稳定状态使被控对象的输出等于参考信号（参考电压或浮子的位置）。