如何提高系统的鲁棒性与敏感性？

在兔种群的例子中，行为的敏感性与内部参数（出生率和死亡率）有关。为了引入敏感性和鲁棒性的概念，我们从其他简单例子开始。

1.静态测量/传感器误差

让我们考虑一个简单的转速表。原则上设备是一个如V=f（ω）的静态模型，其中ω是电动机的旋转速度，V是输出电压。如果转速表的轴相对于我们要测量的轴有滑动，那么将会产生误差：

V+ΔV=f（ω+Δω）

我们称Sω=（ΔV）/（Δω）是转速表的输入敏感函数。通常情况下，它是一个输入函数。如果转速表函数线性的，那么敏感度函数是常函数并且与转速表的增益相等，如图6-10a所示。

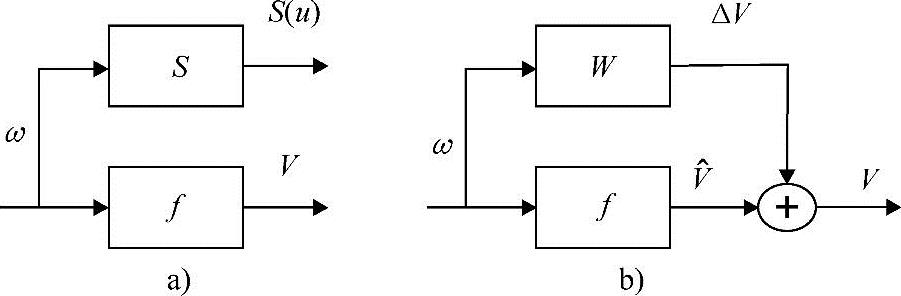
图6-10 静态测量工具的敏感性

实际的测量函数可能与我们认为的函数模型不同。也就是说，测量V=F（ω）≠f（ω）。例如，这是仪器没有完全校正的结果。在这种情况下，我们不知道真实的函数F，但是我们可能知道其中的差异，因为我们知道仪器的校正信息。差异为

W（ω）=F（ω）-f（ω）定义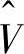为电压的预期值，我们可以用如图6-10b所示的框图表示转速表。函数W（ω）表示模型的不确定性，在这里表示一个额外的不确定性。

虽然两个概念非常接近，但是不是同一个概念。其中一种测量两个函数差异的方法是描述所有可能偏离的最大值。(www.xing528.com)

另一个测量不确定性的模型为

V=F（f（ω））；V=f（F（ω））（6-16）

这里F表示一个函数，与捕获不确定性的个体相接近。左边是理想设备输出的不确定性，右边是直接测量的目标值，即设备的输入。前者可称为输出不确定性，后者可称为输入不确定性。F偏离个体越多表示我们对实际测量原件f的了解越少。在线性系统中，这种不确定可被描述为乘法不确定性。在线性或非线性情况下，它可以被描述为串级系统，只在非线性情况要注意相乘的顺序。

在任何测量设备中都会存在许多导致错误的根源，可能是系统误差或者由于量化导致的随机误差。在所有的控制应用中，知晓所有不确定性的来源是非常重要的。更可取的是不确定性来源的信息可以量化期望行为。

2.未建模动态

让我们考虑一个光盘（CD）播放器，激光束连接到一个由转速极快的电动机（音圈电动机）驱动的臂。电动机的简单模型是从力到位移的双积分器。在这里我们假设臂是刚体，光盘以一个固定而已知的速度旋转，且无外部扰动存在。由于机械共振的存在，真实系统不可能是纯刚性的（快速的动作意味着轻的部分不是刚性的）。另外，机械臂受外部振动的影响，光束与CD旋转轨迹的相对位置会受制于偏离光盘的偏心，偏心与磁盘的大小有关。以上这些都是理想模型不存在的扰动因素。

这些扰动影响CD播放器行为的方式大不相同，这是因为它们频率范围和光谱容量是不同的。CD旋转的离心有定义非常明确的频率，进而能够被跟踪与补偿。机械共振在高频范围是非常典型的，因此只与指针从一个轨道移动到另一个时的快瞬间相关。一般情况下，避免指针移动的快瞬间激发共振就能避免共振。外部的机械波动都是非常低频率的，例如与发声者发出的声音有关。被控系统必须对这些扰动不敏感。

这个例子与3.4节的天线跟踪的例子非常像。

如果我们回到转速表的例子，我们还需要考虑另外一种扰动。旋转机器的刷子在清扫时制造了高频的噪声。这种噪声如果不被滤掉将会反馈给过程并干扰转速表系统的运行。这个问题将在第7章进行讨论。