限制圆和混沌的数学模型探讨

一些系统有不同的平衡点甚至还有更复杂的静态行为。如一个兔子种群的模型（无捕食者），在给定的时刻，兔子的数量为x（k）。食物短缺（老年）等因素会导致兔子死亡。我们假设动物的出生率与死亡率有关，和兔子数量的平方成正比。即为

x（k+1）=r.x（k）-d.x²（k）

如果我们定义一个新变量z，使z（k）=（d/r）x（k），那么新的方程^[12]就只与参数r有关。

z（k+1）=r.z（k）[1-z（k）]（6-15）

很显然有两个可能的平衡点z_e1=0和z_e2=1-1/r（当r>1时该平衡点是实数）。在这个归一化模型中，改变参数r会导致过阻尼稳定平衡点变成振荡甚至是混沌现象。

当0≤r≤1时，会产生过阻尼，并且兔子种群将会灭绝，也就是数量最终变为z_e=0，当1≤r≤3时，会产生欠阻尼现象，兔子种群不会灭绝（除非初始时兔子数量为0），数量最终为z_e=1-1/r。当r=1时，零种群的局部属性会改变，该参数就是分歧参数。

如果r=3，就会存在另一个分歧，所谓的翻动分歧。系统不会达到任何的平衡点，取而代之的是它会以固定周期2进行波动。对于r=3和任意初始条件z（0）<1，最终的种群数量会在0.6179和0.7131之间跳变，如图6-9a所示。几乎所有的种群数量都会达到一个极限圆（除了以不稳定平衡点z_e1和z_e2为初始条件）。

如果我们进一步增大r值，新的波动将出现，r≥3.57时，就会出现混沌行为。在混沌范围内，种群的演变将对初始条件更加敏感，如图6-9所示。图中系数r=3.8，初始条件为z₁（0）=0.5的种群演变用“○”画出，初始条件为z₂（0）=0.5001的种群演变用“·”画出。可以看到在25个周期之后，演变将完全不同，而这种不同（用叉标出）开始越来越明显。(www.xing528.com)

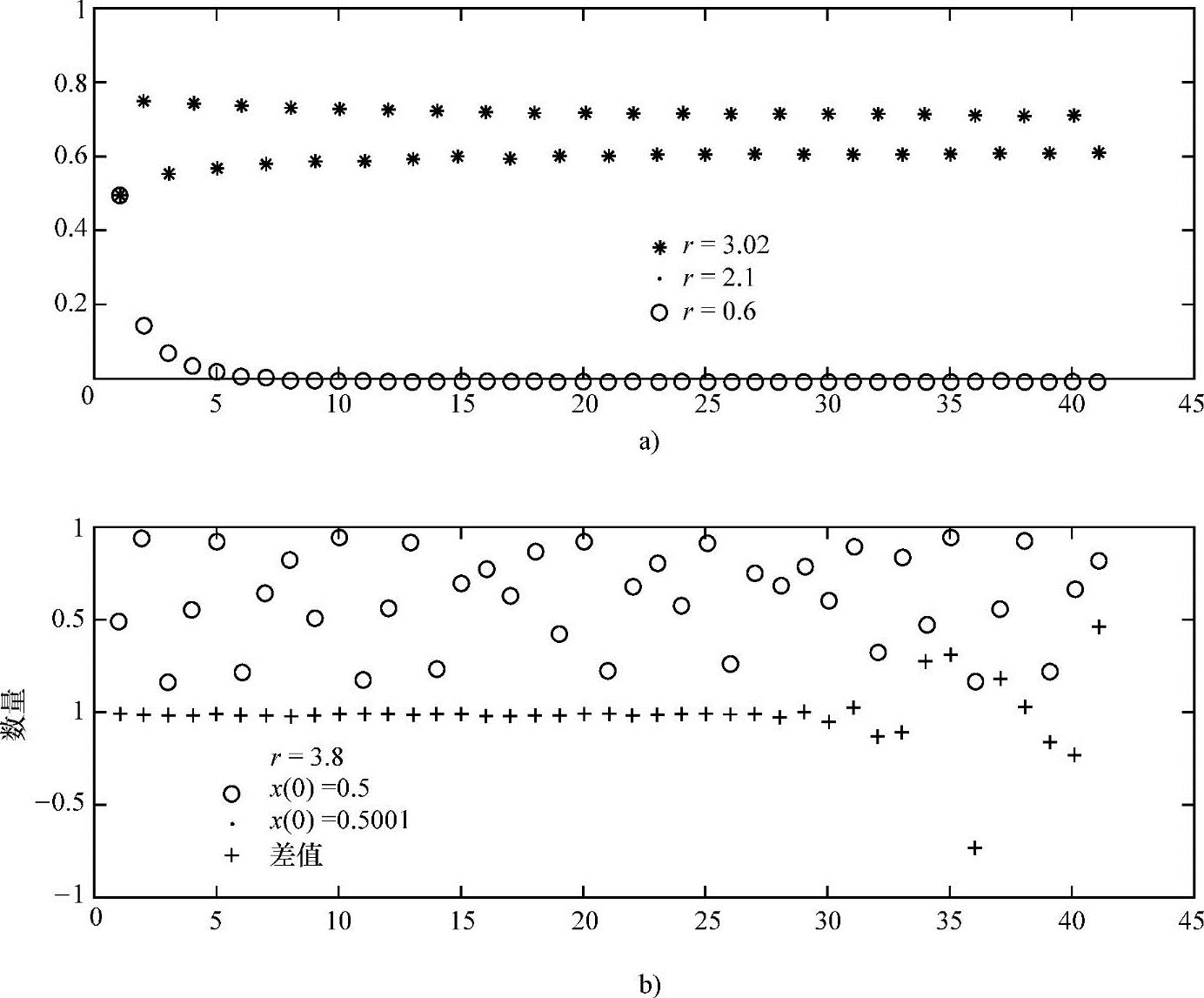
图6-9 兔子种群的混沌演变

a）不同参考系下兔子数量 b）周期数

混沌行为可以按照随机的概念去理解，但不是随机的，混沌行为是完全确定的，因为如果模型和当前的状态已知，那么未来的状态是可以精确计算的。混沌行为的主要的特征是系统演变对极小的状态扰动都很敏感。从这一观点，确定系统的随机解释可能非常有用。

很少有系统表现出如此极端的敏感性。一般情况下，如果系统是稳定的，系统参数、输入信号的小变化或新的扰动会使系统行为产生小的改变。定性的改变，如分歧，只会在很少的情况下出现。

因为分歧很少，所以理解哪些是，哪些不是很重要。正规的系统实验也许不会显示即将出现的分叉点的任何踪迹，想要观察到有趣的现象需要周密的实验计划。