输入信号稳定化和串联优化

考虑串联着的两个系统，如图1-6所示，第一个系统的状态或者输出（y₁=C_1x1）作为第二个系统的输入。

如果第一个系统S₁的输入u和状态（输出）y₁通过增益函数G₁相连，第二个系统（S₂）的输入（u₂）和状态（输出）y₂通过增益函数G₂相连，并且两个子系统都是输入-状态稳定的，那么通过u₂=y₁的全局串联也是输入-状态稳定的，串联系统的输入是u₁，状态为（y₁，y₂）。另外，我们可以估计输入-状态增益函数。串联的增益函数是子系统增益函数的组合。即

G_cascade=G1^G2

很明显，如果两个水箱分别是输入状态稳定的，那么串联后的系统仍然是输入状态稳定的。

我们已经在3.2节和3.3节分别讨论过两个系统串联的例子，陶瓷砖的生产和重力自流灌溉系统。在制造加工过程中，通常每个阶段的输出是下一阶段的输入，自然子系统串联构成了整个系统。类似地，在灌溉渠中上游即时水位会影响下游池的水位，自然子系统（水池）的串联构成了整个系统（渠道）。如果每个子系统都分别是输入到状态稳定，那么可以推断整个系统也是输入到状态稳定。而且我们可以量化子系统发生的扰动对所有下游子系统和整个系统的影响。从这个角度看，输入到状态稳定是一个强大的概念。例如，相同或几乎相同的子系统串联时，单独子系统的输入到状态稳定性很容易得到，那么就可以推断整个串联系统的相关信息。串级系统的稳定性(www.xing528.com)

为了判定串级系统的稳定性，我们只需要分析各个子系统的稳定性即可：假若，每个子系统都是稳定的，则串级系统稳定。假若，任意一个子系统不稳定，则串级系统也就不稳定。

这在线性系统中相当明显。串联系统的传递函数就是子系统传递函数的乘积，这通过框图很容易得到（见5.6.2节）。因此我们将两个串联的子系统表示为

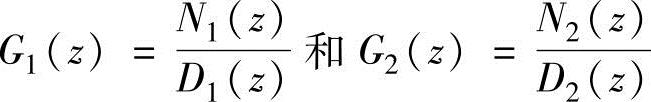
G（z）=G₁（z）G₂（z）表示串联的系统传递函数，很显然传递函数的分母是D1（z）D₂（z）的乘积，串联系统的根是子系统传递函数根的并集。只有当两个子系统都是稳定的，串联系统才是稳定的。