利用ISS方法稳定非线性系统

弄清输入如何影响系统特性的主要困难是变量有很多。为了做一些改进，我们需要限制考虑的可能性。首先我们会问输入的大小如何影响系统信号的大小。在稳定性的文献中，这被称为输入到状态稳定（或ISS），和输入状态增益^[10]（函数）的概念。

通常即使这么简单的问题也非常复杂。例如，在水箱的例子中，如果输入既不是给定也不是流出量而是控制参数α，那么系统中会存在输入和状态的乘积，所以系统是非线性的。我们可能猜想出在这种情况下，一旦输入（α）在区间{0，-2}之外，系统将会变得不稳定。

为了研究一般的情况，我们先研究离散系统的状态空间描述式5-17。

在时间t₀时，初始状态为x₀。我们会根据初始状态和模型方程（这包括时间变化和无限时间的输入函数）计算初始时刻后t>t₀的状态变化，这就是状态的本质。典型的输入输出稳定性形式：

‖x（t）‖≤g_x（‖x₀‖，t）+g_u（‖u‖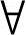），t>t₀（6-13）

这里‖·‖是范数运算，g_x是初始条件大小和时间的函数，反映了初始条件的作用何时消失，我们希望随着时间增加g_x（.，t）→0。而且g_x（0，t）=0。

g_u也是增益函数，它表示输入对状态的影响。我们希望g_u（0）=0同时它是一个增函数，即当0<a<b时g_u（a）<g_u（b），当a<b时g_x（a，t）<g_x（b，t）。通过式6-13我们可以看到在0处存在平衡点。因此，这样的陈述是关于稳定性的一个非常有力的声明。

显然ISS是从初始条件和输入两方面着手。事实上一个适当的ISS必须要有初始条件的稳定性，因为它会将无初始条件作为特例。

ISS描述平衡点稳定性的特性。这是常见的稳定性问题，但不是最常见的。

ISS要求在零初始条件下，平衡点邻域内的所有轨迹在该平衡点附近并会最终收敛于平衡点。ISS涵盖了经典的渐近稳定平衡点的概念。事实上，前面的定义和以上的表述是等价的。

另外，ISS可以处理输入，它表述输入不可能使系统状态偏离平衡点太多。增益函数g_u决定了在输入作用下状态会变成多少，这限制了给定信号作用时状态的大小。这时g_u就好似线性系统中的传递函数。

我们可以回到小球在盆地中运动的例子，假设给位于平衡点a处的小球轻轻的推力，直观上小球会离开平衡点，由于作用力小它会再回到a。然而，如果给小球一个大的推力，小球会越过c点再也不会回来。ISS可以限定式6-13的有效范围，从而涵盖所有这些信息。(www.xing528.com)

我们可以推知基于信号大小的输入状态稳定概念是保守的。绝对值不只是信号的唯一关键的信息。另一方面，因为ISS的信号是一个实际测量值，所以这个方法非常实用，尤其是对于系统互连。粗略地说，从这一观点看，每个系统都被增益函数取代，连接系统的拓扑结构决定了信号大小的变化。这可以使我们很容易验证由满足输入到状态稳定的子系统构成的系统是否还满足这一属性，另外还可使我们量化整个系统的状态到底有多大才能成为所有影响系统外部输入的函数。我们将在下一节讨论这些问题。输入到状态稳定性

由状态空间模型描述的系统（5-18）或是（5-17）被认为满足ISS，对于任意初始状态x₀和有界输入函数u（含有限幅‖u‖），状态x的限定函数如下：

‖x（t）‖≤g_x（‖x₀，t‖）+g_u（‖u‖），t>t₀（6-14）

函数g_x反映系统对初始条件的瞬时影响，它随着初始状态而增加，随着时间推进而减小到0。

函数g_u反映输入大小对于状态大小的影响，它被称作输入到状态增益函数。它必须是非递减函数。

ISS是一种鲁棒的，实际的，非常合意的稳定性概念。特别是零初始条件和零输入时，不等式6-14的右边两项都为0，这表明状态也是0，即x（t）=0是平衡点。而且这是唯一的平衡点。

基于李雅普诺夫稳定性，有很多针对不同非线性系统估计函数g_x和g_u的方法。实际上ISS和李雅普诺夫稳定是息息相关的。

对于状态线性和输入线性的系统^[11]，输入到状态稳定和平衡稳定是一致的。因此，就像以前提到过的，对于线性动态系统，讨论稳定或不稳定系统是非常合理的。对于非线性系统，当然不是对于所有的情况，正如我们讨论过的水箱和山谷中小球的例子。

由于可利用连接系统的ISS推断其稳定性，所以输入到状态稳定是非常有用的。当因果方向明显时ISS特别适用，因为ISS概念默认信息流是从输入到状态，前者影响着后者的将来。当信息流向很清晰时，根据子系统构建系统基本上有两种方法，两个子系统级联或两个子系统形成反馈。

有界输入输出稳定性：

当输出恰好是状态时，ISS称为有界输入输出稳定，简称BIBO。这种概念阐述的思想是有界输入可以导致有界的输出。