李雅普诺夫第二方法：探究能量与稳定性

稳定的研究与能量的概念紧密相连。让我们回忆一下小球受重力的例子，我们会注意到稳定平衡点与小球势能局部最小处相对应，即小球停在谷底；不稳定平衡点与小球势能的局部最大处对应，即小球停在山顶。

如果我们将小球在b处无初速释放，显然小球会获得动能（加速），同时损失势能。小球在b处的势能转化成了动能和与地面摩擦消耗的热量。当小球到达点a，它的势能达到局部最小，动能局部最大。当小球继续滚动，其动能转化为势能，并达到最大位置（势能局部最大，动能局部最小），之后再滚动下来，依此类推。最终，小球在a点静止。通过热力学第一定律，我们知道能量是不会损失的。摩擦会产生热量，热量是由机械能转化而来的，所以小球的机械能，即动能与势能的总和，随着时间不断减少。另外，当小球停在山谷处时，其机械能是全局最小的，所以其机械能有下界，沿着小球的行进轨迹机械能会达到最小。那时小球会停在像山谷a的一个位置，无动能。自然系统会向着稳定均衡发展。（这可与热力学中的最大熵原理相关联，最大熵原理是Gyftopolous和贝瑞塔1991年发现的。）

对于大多数的物理系统，系统总能量尤其是其能量随时间的变化是了解系统稳定性的极佳的开始。对于复杂系统，或者不属于物理的动态系统，如社会和经济系统，不大可能用能量观点解决问题。为了克服这些困难，李雅普诺夫已经完美地将能量的思想推广到任意的抽象系统中。这就是李雅普诺夫对运动稳定性的第二个重要的贡献，称为李雅普诺夫第二方法。利用李雅普诺夫第二方法解决稳定性问题

考虑所涉及系统的平衡点x_e。假设存在一个系统状态的能量方程V（x），在平衡点附近V（x）≥0，以至于只有在平衡点处此能量会消失。我们由此捕获了一个概念，即波谷是一个平衡状态。

如果一个系统中，所有以初始状态x₀（在x_e附近）为起点的沿着轨迹运行的函数变量V（x（t））都不随着时间增长变化，这样的系统就是稳定的。

在李雅普诺夫第二方法中，对系统稳定性的判断转化为寻找具有以下特性的能量函数V（称为李雅普诺夫函数）：函数有下界（平衡点处最小），并且随时间变小。如果能够找到这样一个函数，那么可推知系统是稳定的。

当问题中的平衡点稳定，这样的李雅普诺夫函数一定存在吗？我们得知道寻找这样一个函数不是徒劳的。李雅普诺夫称如果一个平衡点（局部）稳定且具有吸引能力，那么就会有这样的李雅普诺夫函数存在。尽管如此，这个存在定理并不会为我们寻找李雅普诺夫函数提供任何帮助，因为基于存在定理构造的李雅普诺夫函数需要包含系统的所有轨迹，如此一来很难计算。

李雅普诺夫第二方法或称为直接方法的缺点就是难于寻找李雅普诺夫函数。没有找到合适的函数意味着无法证明任何东西。(www.xing528.com)

李雅普诺夫的思想是不用计算系统的轨迹，不用掌握系统的准确信息就能知道系统是否稳定。因为事实上我们需要的就是寻找到标量李雅普诺夫函数V，其值随时间下降。不用计算所有解，李雅普诺夫函数就可以包含所有信息（至少是感兴趣的平衡点邻域的信息）。在我们不知道解的情况下李雅普诺夫函数是可以建立的。假设系统描述为普通的微分方程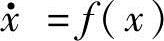。我们可能无法求解它，但是我们需要判断是否有一个函数V随时间减小，所以我们要做的是求V对时间的导数，如下：

非线性系统举例

考虑如下式定义的系统：

李雅普诺夫方程为

V（x）=x²

由于除零为平衡态以外，它总是正数，此外‖x‖随着V（x）增大而增大，时间的倒数V在解决方案上满足：

上式除了平衡点以外总是负值。平衡状态是稳定的，甚至渐进稳定，由于我们在计算上没有限制，我们就可以决定大范围渐进稳定的稳定性。