探索稳定性及稳定性的分析介绍

在设计控制系统时，需要满足的最低标准就是稳定性。因此，理解稳定性属性与系统参数的关系是非常重要的。稳定性是一个敏感的属性吗？参数中的一些变化会导致系统稳定性的改变吗？小球在山谷中运动的例子说明这可能不是问题。另外，如果系统是不稳定的，控制的主要目标就是使不稳定的系统变为稳定的系统（就是我们必须对原来山峰的位置进行改造）。当参数变化时，系统的某部分可能从稳定的变成不稳定的。这是为什么，当系统参数变化时对于特定系统究竟发生了什么，这是分岐理论的内容。通常情况下系统行为曲线会随着参数变化光滑地变化，除了一些参数的特殊组合。在这样的分歧点附近，诸如稳定性这样的定性属性会突变，这是因为均衡会以一定的方式创生、消失、交互。

1.一个例子

我们回忆一下第2章水箱的例子，具体可以参考2.4.4节。

一个水箱可描述为

x（k+1）=x（k）-c（k）+u（k）；u（k）=α（x（k）-r）（6-9）

式中 x（k）——在k时刻的水的体积。

c（k）≥0——从k到k+1时刻水箱流出水的体积。假设它与水箱中水量无关。

u（k）——从k到k+1时刻流入水箱水的容积。

r>0——水箱的给定容积。

α——根据水箱中水容量调节的控制参数^[6]

假设一个采样周期水箱流出水的体积c（k）=c>0是常数，水箱的期望水体积r也是常数。我们将基于控制参数α分析水箱的行为以及α影响系统动态的方式。

再次写出系统的表达式：

x（k+1）=（1+α）x（k）-c-αr（6-10）

平衡点

平衡点x_e满足下式：

c

x_e=x_e-c+α（x_e-r），orx_e=+r（6-11）

α

上式的物理解释是在平衡点，通过u（k）=α（x_e-r）控制输入水箱的水量能与流出水箱的水量c保持平衡。在这种情况下，水箱的水量保持不变。注意这意味着平衡时的水面液位不可能与期望液位相同（等式6-11）。基于反馈（水箱液位相对于期望液位）的控制量u（k）只有通过偏差x_e-r≠0才能进行正确的控制。

式（6-10）可写成另外一种等价的形式：(www.xing528.com)

（x（k+1）-x_e）=（1+α）（x（k）-x_e）（6-12）

这种形式可以清晰地展示出水箱中水体积与平衡点偏差的变化。

2.设计问题

设计问题是：什么时候平衡将会是稳定的？我们怎样选取参数α，才能保证系统的稳定性，同样使水箱中的水体积收敛至给定值^[7]？

要想使平衡点x_e收敛至目标值r>0，需要将α（或正或负）设得很大，但是为了稳定，线性系统（式6-12）的极点1+α必须小于单位值，这限制了α的范围，见6.4节。

0>α>-2

稳定性的条件是负反馈α<0。如果水的体积太大了，比如x（k）-r>0，那么当α<0时u（k）会使水流出水箱。

一种非常特殊的情况，称为“死拍”控制，就是指在α=-1时，经过第一拍之后系统就达到平衡。

如图6-7所示画出了当α=-1.5时水位的轨迹。α值不同时，图类似。在图中，α值的变化可以通过非对角线的斜率反映出来（这可以当做一个练习）。

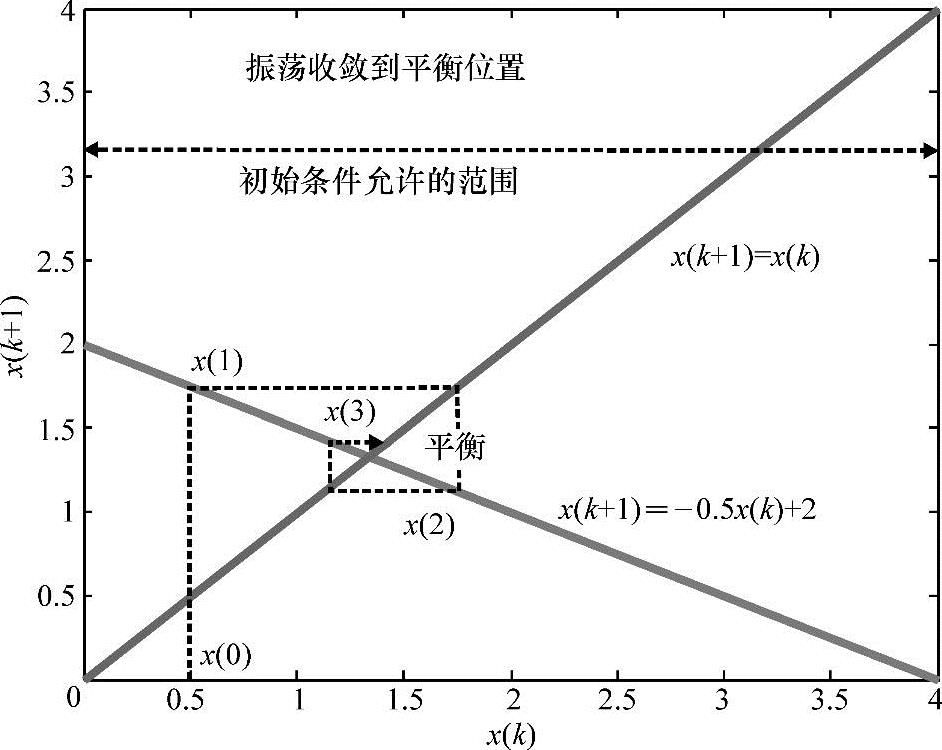
图6-7 -1>α>-2时水位振荡行为

3.分区

这个例子的重要之处是说明了如何通过反馈将稳定系统变为不稳定系统，以及这个变化是如何发生的。这些现象可被总结为一张图，就是如图6-8所示的参数平面。这张图表示了对于系统特定的定性行为给定水位r和控制参数α的所有可能选择。这张表称为分岔图。它能够识别出参数空间中系统（更准确地说是系统的轨迹）定性属性发生突变（或者分叉）的位置。

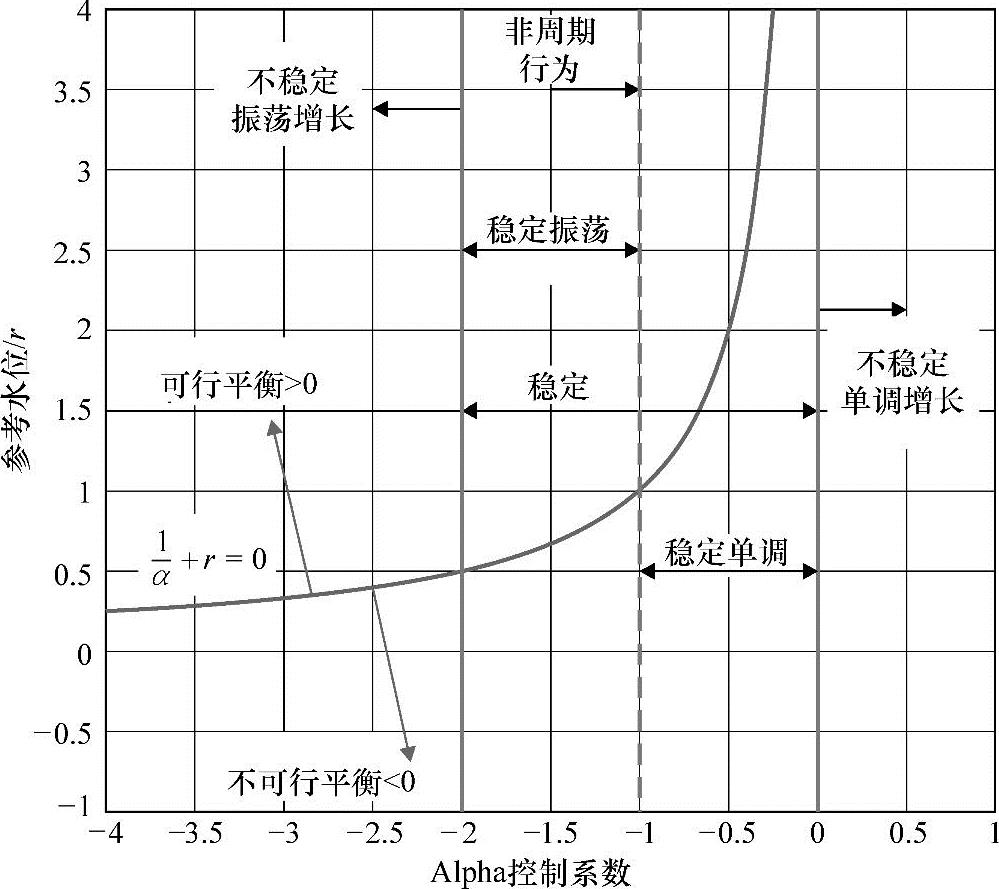
图6-8 恒定排水量c=1时水箱液位变化，水位参考变量r和控制参数α

通过这个例子总结如下：

●稳定性在离散的参数值下变化（这里α=0，-1，-2）。除了这些特殊的条件，参数的小变化只会影响轨迹、稳定性和性能属性，这很具有普遍性。这是分区理论的一个基本观察结果，分区理论是理解这些特殊点，并通过整理关联我们可以清晰地知道动态系统的轨迹发生了什么变化（或者将要发生什么变化）。

●例子中的动态系统是线性的，然而在下一章中的讨论，我们会发现基于哈特曼-格罗伯曼定理非线性系统的平衡会继续存在这些结果。在平衡点的邻域，线性系统可以近似表示大多数局部行为和非线性系统。

●稳态响应（这里指平衡时水平和期望水平的偏差）和暂态响应（这里指到达平衡的速度）是耦合的，但是它们不会齐头并进，这存在一个权衡。好的稳态响应需要很大的α，但是能保证稳定性的最大α值是-2。而且α越接近-2，暂态响应越慢，也就是需要更多的时间到达平衡点。由于系统结构太简单，所以不允许我们设计暂态和稳态响应。对于供给率更精确的控制需要避免或者改善权衡。然而，也正是由于需要权衡才使得控制设计非常有趣。