自治系统稳定性分析与优化

稳定性的概念最早出现在力学，当时是研究三维空间物体的运动（比如机器人或卫星的运动）。稳定性是一个依附于具体系统响应（运动）的自身属性。在特定的情况下，当有一个小偏移（位置或速度）出现时会发生什么呢？后续的变化会与未发生偏移时的响应相同吗？如果是，我们称响应（运动）是稳定的；如果不是，响应（运动）是不稳定的。

通常我们只针对特定的系统响应才讨论这个特性。有时没有混淆的可能，我们称系统是稳定的，意为系统的任何响应都具有这个性质。

考虑一个在起伏地形运动的球的例子，球在运动时受到重力和滚动摩擦力，如图6-3所示。这里的系统是球受到重力在地面上滚动。如果我们假设球总是贴着地面，它便具有纵向位置和速度的特性。

直观地看，山谷的最低点是个特殊点，如图6-3所示，就是所谓的平衡点处。

如果球最初在这个位置不动（不具有初始速度），除重力和摩擦力之外无其他力作用（表明球在水平方向的加速度为0），那么我们可以通过牛顿定律判断小球将在该位置静止。在该位置的一个小的扰动（在该位置轻轻地触碰小球或者给小球一个初始速度）不会令我们担心，球总会在该平衡点附近运动，并且最终会回到平衡位置。我们将a点称为稳定点。

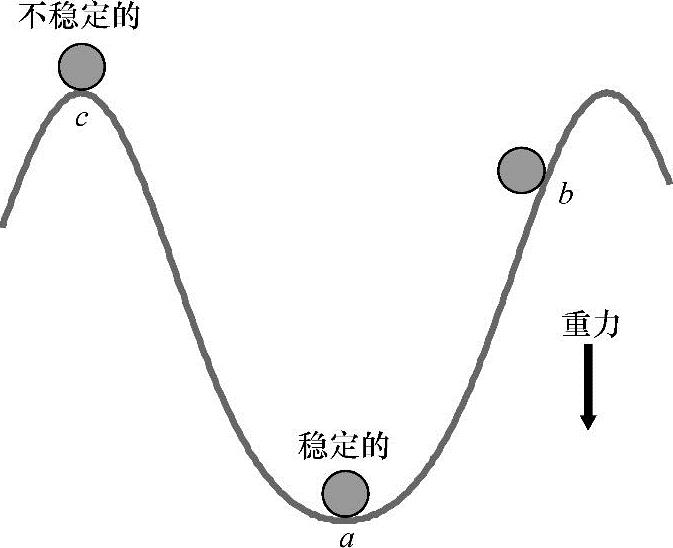
图6-3 位于起伏地势的受重力（假设重力方向从上自下）的小球

而位于山顶端的c点也是一个平衡点，但是它与平衡点a不同。一个很小的扰动（一个水平方向的非零速度或者水平方向小的推力）都会使位于c点的球掉下并且远离c点不再回来，我们将c点称为不稳定点。

当小球从初始位置b无初速度释放，小球将会受重力作用滚下来并且在点a点做往复运动。因为小球受摩擦力，所以将会停在a点。我们说a点是一个稳定的吸引平衡点。显然a点只是一个局部的稳定点。事实上，如果我们给球一个足够大的初速度，那么球将会经过c点永远不回来。

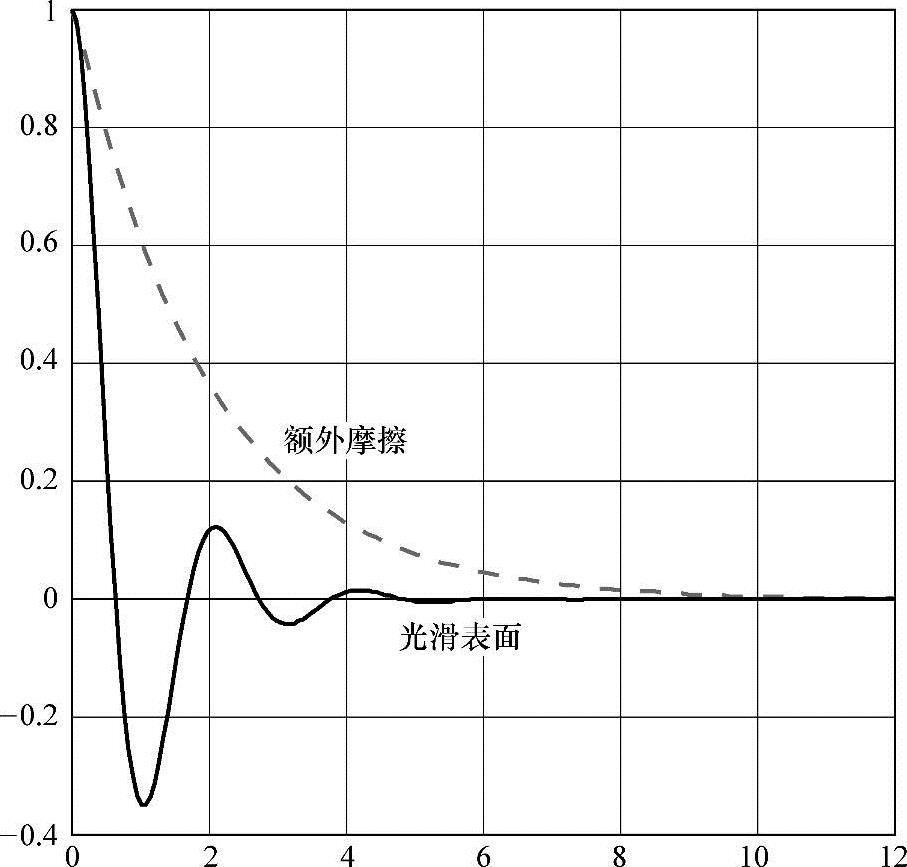
球的轨迹在水平x轴的投影将会很大程度上取决于球和滚动地面之间的摩擦因数。球轨迹可能是摆动的；如果摩擦力小，球的轨迹是阻尼振荡的；如果球滚动时损失很大能量，球的轨迹也可能不是摆动的。如图6-4所示。

(www.xing528.com)

图6-4 从同一点出发受到不同摩擦力的小球的轨迹

稳定性（不稳定性）是一个局部的属性，是对小球在特殊位置（这里是平衡点）运动行为的定性描述。它考虑了小球未来的运动，所以从时间的观点看，它是一个全局的属性，这使得稳定性很特别。从这个例子可以看出，稳定性在运动空间是一个局部的属性，因为小球有很多具有不同稳定性质的平衡点。

平衡点a有较强的稳定性。首先，可以在初始点施加扰动，给小的初始速度或给小的推力使球到达a点的附近。无论任何情况，小球会在a点附近运动，轨迹最终都会收敛于a点。这样的平衡点称为渐进稳定点。渐进稳定点不仅需要平衡点是稳定的，还能够吸引在附近运动的物体运动到该点。自治系统的稳定性

考虑一个动态系统，即描述系统中所有可能的初始条件的响应集合。

平衡指的是不变的响应。

如果在任意接近平衡的初始条件下，相应系统轨迹在未来任何时刻都与之接近，那么我们认为平衡就是稳定。

如果在任意接近平衡的初始条件下，随着时间的推移，相应系统的轨迹收敛于平衡态，那么我们称这个平衡态是具有收敛性的。

当平衡既稳定又具有收敛性时，我们称这样的平衡为渐进稳定。

如果初始状态没有限制，我们称系统大范围渐进稳定。

在系统运行未来某个时刻，一个极小的初始偏差只导致了一个极小的运行偏移，那么这个运行轨迹（系统的响应）是稳定的。如果随着系统性能的增加，之后时刻的偏差逐渐消失，我们称这个系统是渐进稳定。