线性系统的状态空间描述

到目前为止，我们已经针对线性时不变系统充分探讨其输入输出的关系。在系统稳定这一假设下，输入输出关系可以用传递函数表示。但是传递函数这种表示方法太简洁，隐藏了系统内部工作机制的细节。

然而，当写系统的方程时，如果不只考虑输入输出的关系，那么必然需要引入其他变量。考虑如图5-9所示的方框图，当初始条件为0，分别定义积分器的输出变量为x_i（i=1，2，3）。如果我们也引入积分器的输入（相应输出的微分），就可以很方便地将框图的方程写出。那么方程为

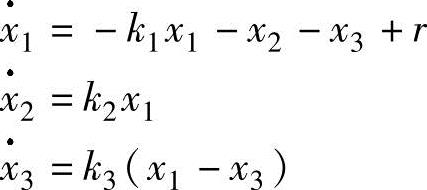
这些方程描述了积分器、增益、相加点和连接。而且系统的输出是

y=x₂+x₃

这些方程不仅包含了传递函数描述的输入输出关系，还描述了整个系统的特性。而且，它们适合计算机仿真。变量的集合{x}成为系统的状态。通过这些方程能够得到传递函数。它足以取代变量s（或jω）构成的表达式，而且可以消去状态变量转换为传递函数模型G（s）。

写下方程，消除变量，找到能够表示系统全部特性的标准方程形式，这个过程称为行为理论（PoldermanandWillems1998）。

更一般的情况，n个线性微分方程的集合可以简化成矩阵形式。

变量x是一个表示状态的列向量（x₁，x₂，…，x_n），系数矩阵A称为系统矩阵；B是列向量（b₁，…，b_n）称为输入-增益向量；C是行向量称为输出-增益矩阵；D是标量表示输入对输出的直接作用。系统矩阵表现了系统的内部结构，并决定了很多基本的性质（见下章）。而输入-增益和输出-增益矩阵能够通过增加、删减、修正一些执行器（用于控制）/传感器（用于测量）来进行修改。直接耦合（D）通常为0。从输入输出的观点看，矩阵（A，B.C，D）的集合等价于传递函数^[13]。(www.xing528.com)

通过状态空间模型，我们可以计算整个系统的行为.如果已知u（t）=0，初始状态x₀=x（t₀），那么就可以计算系统状态随时间的变化，这称为系统的自由响应。在处理自治系统时，这是非常有趣的。另一方面，如果初始条件不存在，那么系统对于某给定输入的响应—动力响应是可估计的。这正是我们通过传递函数得到的系统输出。

状态变量具有以下有趣的性质：

●记忆性：状态是过去的总结。通过过去的状态和未来的输入可以计算未来的状态。

●动态性：输入直接影响状态向量的导数（变化），所以状态的当前值与输入的当前值无关（也不可以通过状态的定义）。

●完整性：如果状态的当前值、输入的当前值和未来值都已知，那么我们可以计算出任何内部变量。

●非唯一性：状态表示方法是不唯一的。给定一个状态表示，我们可以通过坐标变换（同一空间不同性质的表示），或增多变量的个数（状态向量的任意线性组合可以添加到状态中）得到一整类同等的表示，这并不改变系统的输入输出描述。

●最小维数：状态向量具有最小维数，其他所有形式的维数都比状态空间的维数多。

通常情况下，我们可以使状态向量代表简单的物理意义。在任何的机电系统中，我们可以将状态看成是储存的能量。在机械装置中，状态可以被看成动能或势能；在电气系统中，我们将状态看成电能存储器件的电场和磁场能量。如图2_-13所示中弹簧球的例子，如果球的位置和速度在任意给定时刻都是已知的，那么其行为可以完全确定。这两个变量被定义为状态向量，请注意这些变量表示动能和势能。这种属性同样也用于分析系统的行为。在许多其他的例子中，比如世界经济系统的描述，状态可以没有任何实际的物理意义。