线性系统合成方法：实现理论

到目前为止，我们讨论了线性系统分析的工具。对于一个系统既可以计算出系统的时间响应，还可以算出频域响应的幅度和相位。对于一个复杂的模型，我们可能通过简单系统组合的方法重现系统吗？或者存在线性系统能够满足我们期望的性质吗？

例如，我们在第4章曾经讨论过反失真滤波器。通过以上的概念，我们可以很容易地知道这类滤波器应具有什么样的性质。假设采样周期为h，或说采样频率为1/h。根据信号的采样准则，被采样的信号的频率不能高于采样频率的一半。所以，理想的反失真滤波器（如图5-15所示）是一个幅值响应为

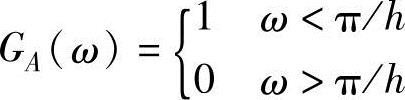
的线性系统，当ω<π/h时，Gφ（ω）=0。所以实际上我们无法建立具有以上性质的线性系统，这其中主要的问题就是传递函数不是一个有理函数。虽然，我们无法准确实现，但是我们可以建立一个符合我们所有实际目的的近似有理函数的。一阶滤波器就是一个非常简单（普遍）的近似。如图5-15所示是一个低通滤波器（G（s）=π/（s+π））的伯德图。

如果一个系统的传递函数能够以参数s（或jω）写出一个合理的有理传递函数^[12]，那么我们就可以通过纯增益和纯积分器的连接将系统构建出来，正如前面的例子一样。这可以从代数基础理论中找到依据，它指出任何含有实系数的多项式能够被分解成含有实系数的一阶和/或二阶的多项式。如图5-9所示的每个部分就是一阶的。

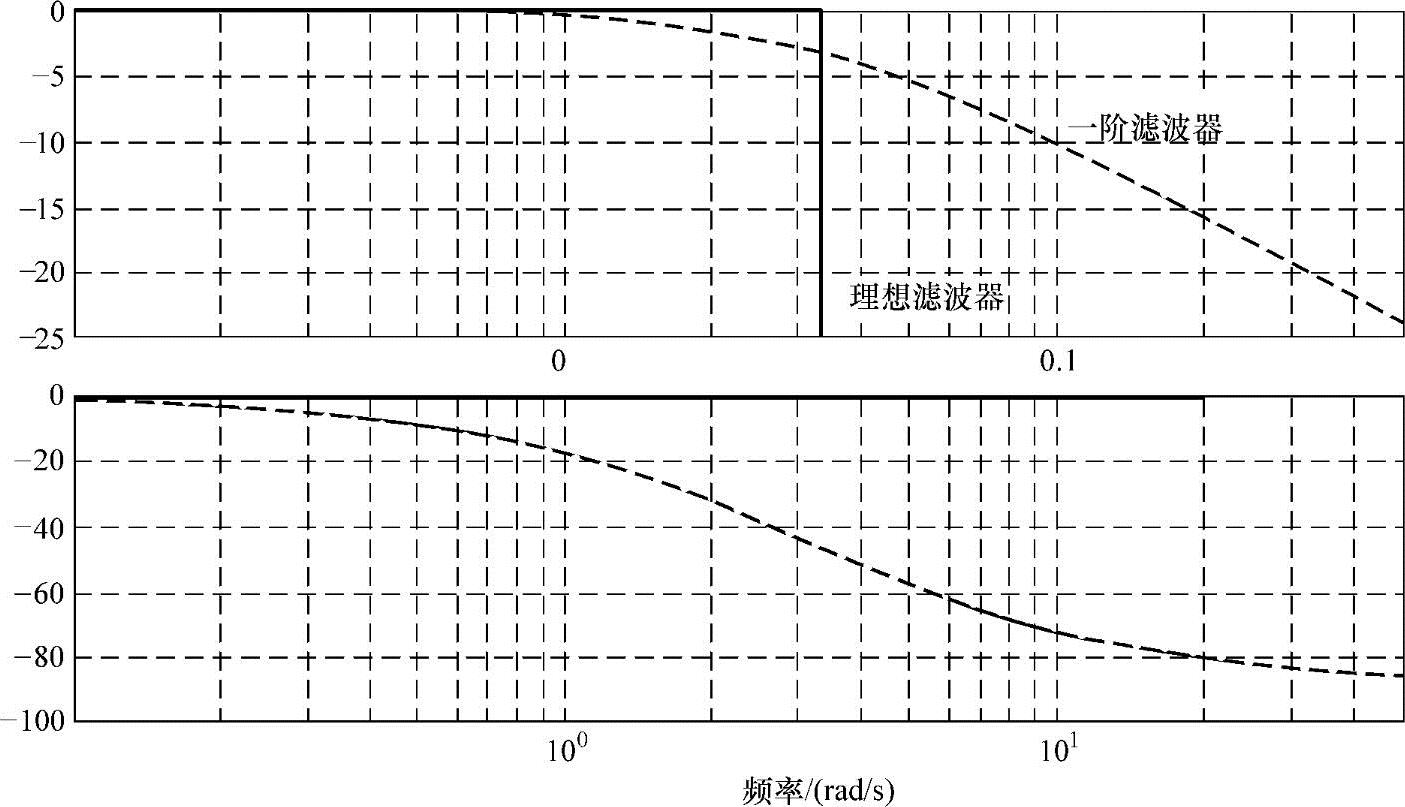
图5-15 反失真滤波器的理想情况和实际情况

(www.xing528.com)

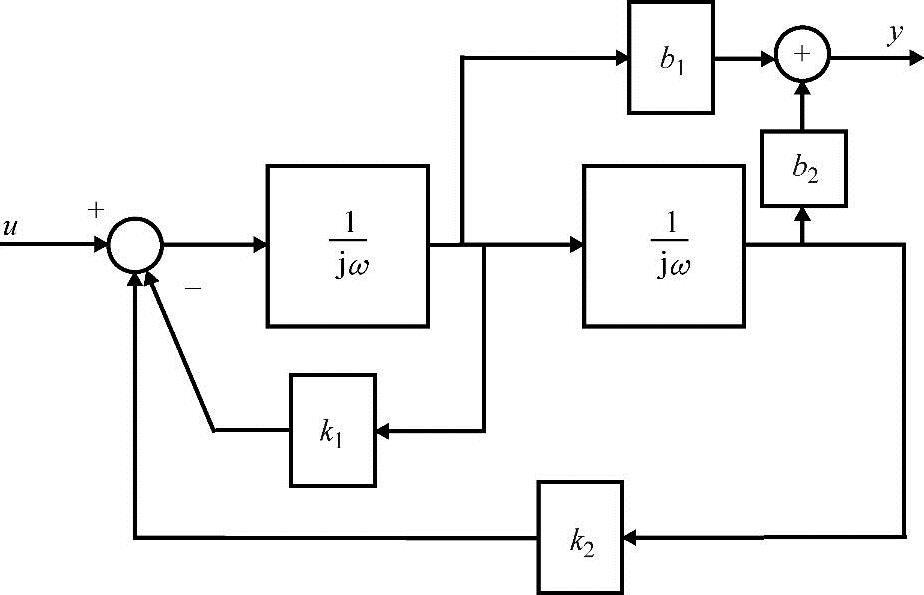
图5-16 二阶有理传递函数频率响应的一般实现

如图5-16所示是一个二阶系统的框图。很显然，通过一阶和二阶基本部件的适当连接，任何含有实系数的有理传递函数及其对应的频率响应都可以实现。这并不是实现有理传递函数的唯一之路。正如许多不同实现方式一样，有理函数也有许多不同的表现方式。尽管如此，通过对当前方法的观察和推断，我们可以得到一个很有意思的现象。分母阶数为n的有理函数需要至少n个积分器实现。很显然当积分器的个数不能少于n。这种方法只提供了恰好用n个积分器的方法。所以，从某种程度上，该方法提供了一个系统最小实现的方法，即用最少的积分器实现传递函数的方法。

其中，G（jω）=（b₂+b₁（jω））/（（jω）2+k₁（jω）+k₂）。

还有更多组合的手段。通过积分器/增益网络组合成传递函数的这一研究称为实现理论。它在电子电路理论中很重要。当用于实现传递函数模块的参数受到限制时，这种组合或实现的问题变得尤为复杂。这种限制包含了对增益的限制（例如只允许正实数），或能量损耗限制，亦或是精度的限制（例如某一区间特定参数的离散模块）。那么组合的难题就是要用不准确的方框图构建一个十分准确的期望传递函数，这个领域仍然有很多没有解决的难题。

第二个关于合成的问题是如何在满足特定参数条件下选择一个匹配的模型。这也通常被定义为设计问题，我们会在相应的章节讨论。

控制设计的真正问题也许从观察的角度能得到更好的解释，那就是控制的全部内容是设计逆操作。事实上，如果我们期望输出y跟踪一个给定的信号r，那么我们需要寻找输入u，使其满足y=Gu=r。在频域G只是一个简单的乘法，所以u=G^-1r就是我们想要的输入。对于这种看法的问题就是可实现的传递函数的逆G^-1通常不存在。第一个原因，如果G是严格因果的（这是我们所期望的性质），那么G^-1就不是严格因果的，那么很显然我们不能通过因果元件构建非因果系统。也就是说，控制问题就是在一类可实现的传递函数中寻找一个关于G^-1r表达式的好的（简单的）近似。这就是逆问题。这种问题是否能处理好取决于同样重要的两点：需要跟踪信号r的类别和传递函数G的特性。