串联积分器并加反馈控制

在前面的5.7中例子已经介绍了带反馈的积分器。如果是正反馈（K<0），响应将变得离谱。很显然，积分器积累输入，正反馈下输入变大，导致积分器更大，如此循环是不稳定的行为（将在第6章讨论）。在物理世界中，这类情况一定会有不良后果的，通常情况下是积分器饱和（溢出，爆炸或者类似的情况）。这类问题如图5-14所示。

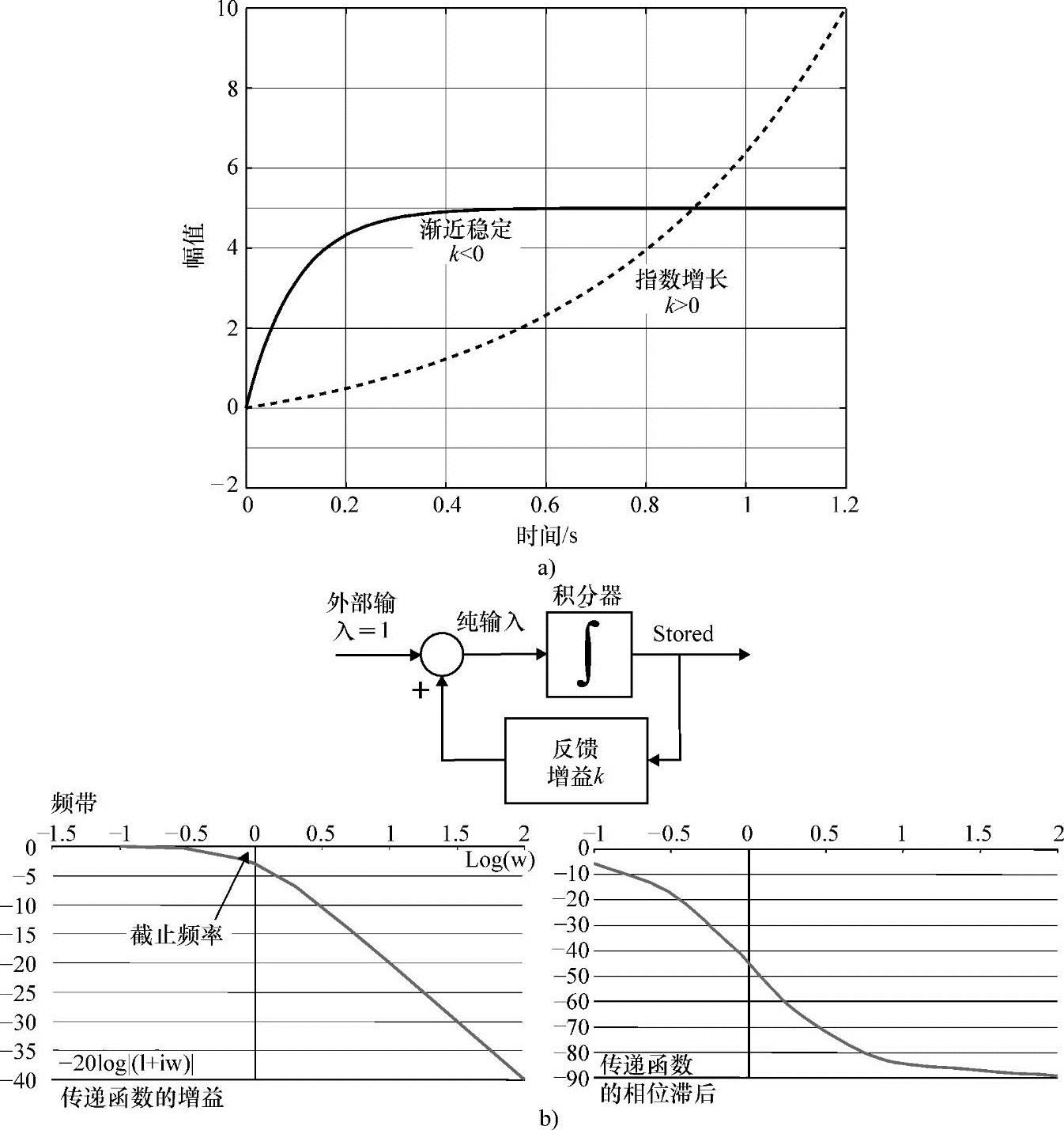
图5-14 积分器加反馈：a）正反馈和负反馈的阶跃响应 b）负反馈的频率响应

相反，具有负反馈的单个积分器则具有很好的特性。系统由单位负反馈回路中的积分器组成，其波德图如图5-14b）所示，在低频段增益是一致的（0dB），超过了截止频率（转折频率）后，增益以-20dB/dec的斜率下降。

在一个负反馈环里，两个积分器会产生自发振荡。无需任何输入激励，只要其中一个积分器在非零的初始条件下，输出就会产生振荡，这类系统被称为谐振系统。当输入频率与系统振荡的频率相匹配时，输出就会无限增长。输入很小，输出扩增的系统就是近似采用这类系统，例如钟摆。(www.xing528.com)

在一个反馈环（正或负）的三个积分器则产生指数型的振荡，这是不稳定的响应。

这些例子说明了系统连接时会遇到一些麻烦，在我们讨论稳定性和灵敏度的概念时，会再回到这个问题上。总体来说，如果系统是稳定的，利用前面提到的频域的方法会很奏效。

当然对待反馈还是要小心。