积分器的频域响应及伯德图与奈奎斯特图的解析

研究线性系统时，通常用正弦信号作为输入。为了描述输出跟踪正弦输入信号的特性，我们需要考虑在每拍内输出的幅值和相位的变化。另外，由于任何信号都可以近似成多个正弦信号的总和，这一条件使我们能够充分地了解大多数的线性系统（要记住所有输出作用时的响应等于每个输入单独作用时响应的总和）。

这种对于线性系统的分析方法称为频域响应分析。这种方法能在控制工程领域广受欢迎的原因是伯德^[11]工程设计工作的成功。伯德基于频域分析的理论，给出了一系列的设计方法，包括放大器、滤波器和第一次被应用于无线通信网络的反馈补偿器。波德研究工作的主要后续影响是他通过波德积分方程描述了在什么样的基本限制下，线性反馈系统能够达到的预期目标。

例如：增益系统和积分系统的频域响应相当简单：

1）简单增益系统的频域响应是一个常数，也就是说增益系统对于任何频域都没有相位转移和幅值变化。

2）对于一个积分器，它的频域响应写成G（s）s=jω=1/（jω），其相位恒为-90，其增益与频率成反比。

另外一个频域响应分析非常受欢迎的原因就是频域响应可以很好地通过图像展示出来，便于计算。在今日，这些工具只有教学价值。

频域响应的伯德图和奈奎斯特图（式5-10）表示了系统的幅值和相位的变化，奈奎斯特图（见图5-12b））仅仅是频域响应（对所有时域的ω，在复平面点的集合G（jω））的极坐标表示。如图5-12b所示，增益G（jω）和相位φ（jω）都是针对具体频率ω画出的。伯德图（见图5-12a）将增益和相位在频域表示出来。画幅频特性的时候，频率的坐标单位是log₁₀w，增益的坐标单位是20log₁₀G（jω）dB。同样，相频特性绘画时相位角∠G（jω）的横坐标的单位也是log₁₀w。

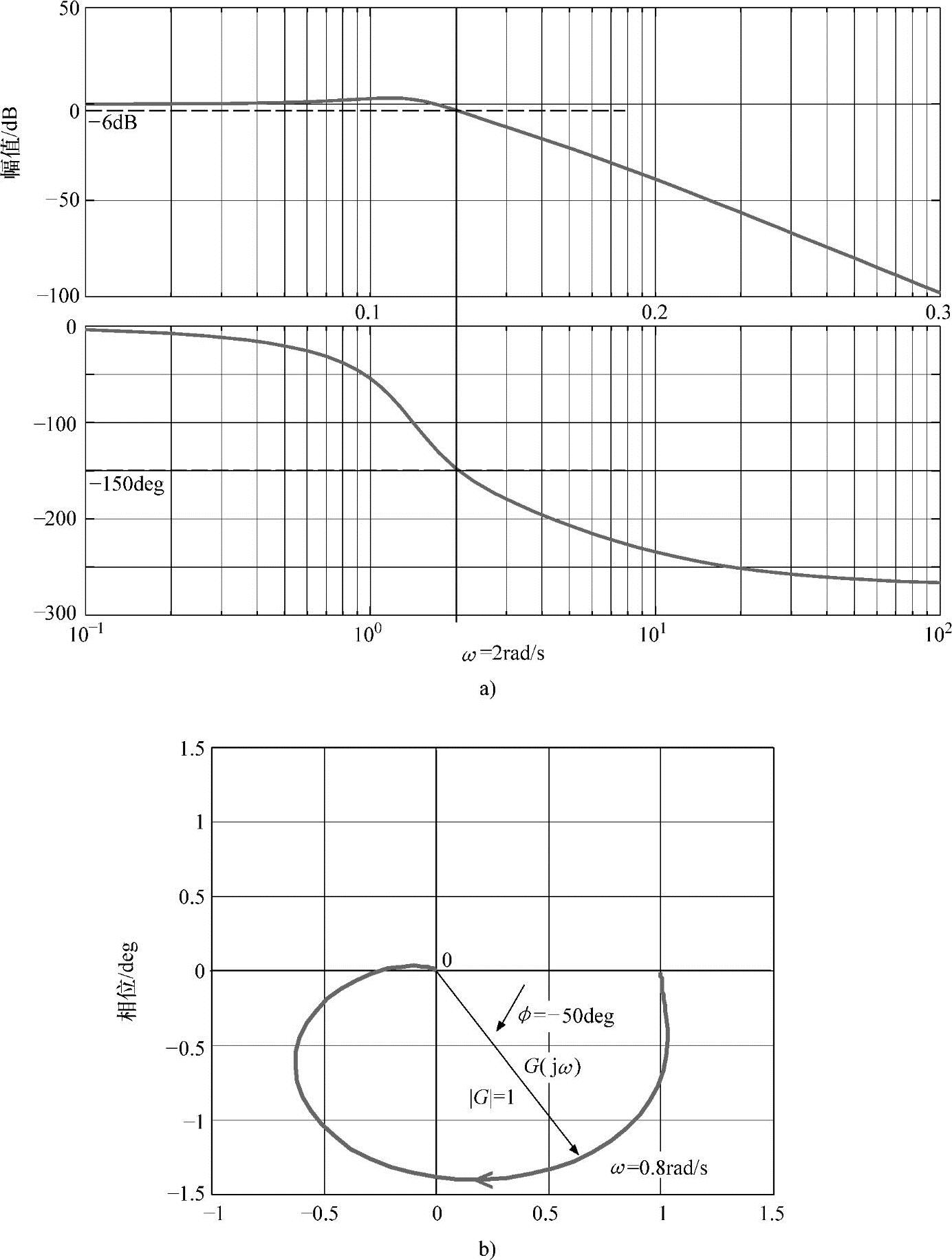
图5-12 频率响应图(www.xing528.com)

如图5-12中所示，有一个幅值最大值处，频率在1rad/s和2rad/s之间；频率在2rad/s之前，增益始终大于1，这段频率称为系统带宽（在带宽之外，输出信号的能量比输入信号的能量的一半还少）。频率大于2rad/s的信号被认为被系统完全抑制，这种系统称为低通系统。

在非线性系统中，应用于分析正弦信号的谐波分析具有很高的价值。显而易见，非线性系统的输出就会包含谐波，甚至是子谐波。另外，将信号分解成线性信号组合以便更好地理解输入的这一方法已经不再适用了。

例子：微阻尼机械臂

我们考虑应用于空间探索的微阻尼机械臂的高度简化模型，输入是手臂的转矩，输出时手臂的位移。伯德图如图5-13所示。

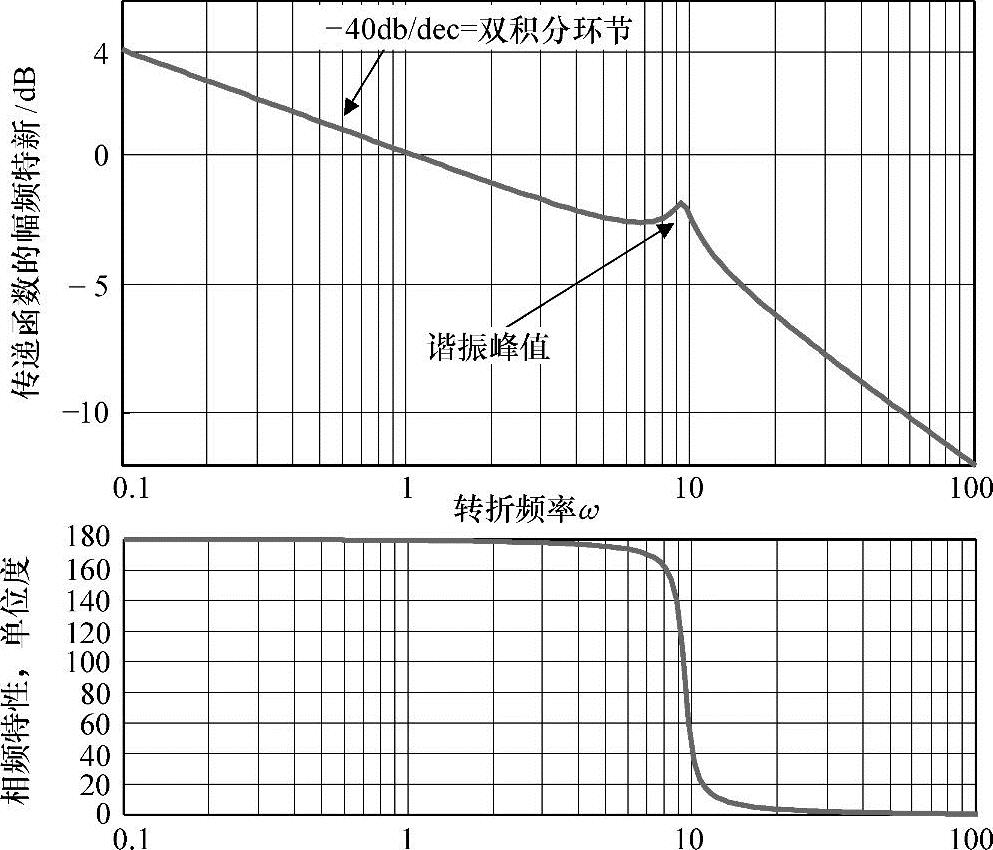
图5-13 传递函数的伯德图：微阻尼机器臂的转矩-位移响应图

伯德图无需广泛的建模，用实验方法就可以得到，这是它的一个优点。我们运用一个信号发生器输入信号，不断地改变信号的频率，同时记录输出信号，很快就可以得到波德图了，频谱分析人员经常采用这种精确的做法。

如图5-13所示幅值的峰值表是机械谐振。初始斜率大约是-40dB每十倍频程，同时初始相位接近180°，这相当于一对串联的积分器（每个积分器的相位滞后90°，即-20dB/dec）。这可以通过牛顿动力学方程得到验证，转矩与加速度成正比，或者说位移是转矩的二次积分。共振添加了额外的180°的相位滞后，所以相位最开始是180°，而后随着频率的增加衰减到0°。