线性系统的框图联结优化措施

线性时不变系统I/O操作器的主要优势点就是可以方便地建立复杂系统的模型、处理框图的变换。这一切都源于一个事实，即线性系统保留了输入的频谱内容，由于是线性的，所以我们可以分别处理每一个输入的频谱。有了传递函数模型，线性系统就可以用方框图相乘表示。

在这种情况下，图、表、框图不只是作为建立交流系统结构的有力的工具，还是一种可以帮助我们迅速了解识别输入输出关系的计算工具，至少在传递函数操作器里，在频域范围内是这样。方框图的变换可以让我们以相对于复杂的积分，在图表里面的操作器可以更直观地表示更复杂的系统的运算地表示出来。

方框图主要有以下三种结构：

1）串联：对于两个相串联的系统G₁和G₂，表示二者相乘：G=G₁G₂，如图5-8a）所示。

2）并联：对于两个相并联的系统G₁和G₂，表示二者相加：G=G₁+G₂，如图5-8b）所示。

3）（负）反馈：系统G₂作为G₁的负反馈，如图5-8c所示。即

G=G₁/（1+G₁G₂）（5-13）

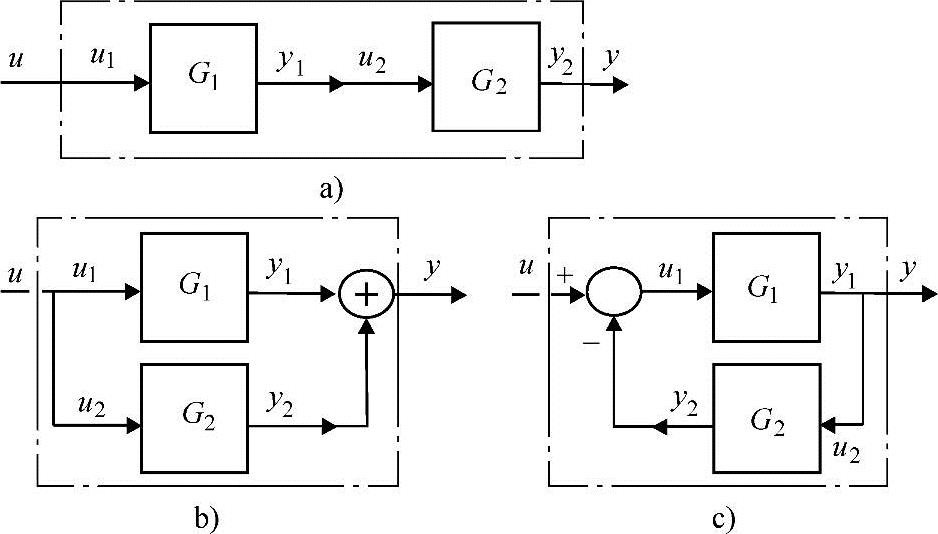
图5-8 方框图举例

a）串联或级联连接 b）并联连接 c）负反馈

这些结构与前面提到的连接的结构相同。如图5-9所示。

系统由三个连接的部分构成，每一个部分都含有一个积分器和一个增益，基于前面（图5-7）的推导，我们可以很容易地分别写出三个部分的输入输出传递函数：

1）部分1的传递函数：E₁（s）=（1+K₁/s）-1（1/s）=（s+K₁）-1；

2）部分2的传递函数：E₂=K₂/s；(www.xing528.com)

3）部分3的传递函数：E₃=（s+K₃）-1（K₃）。

因此，可以简化成如图5-10所示的框图。

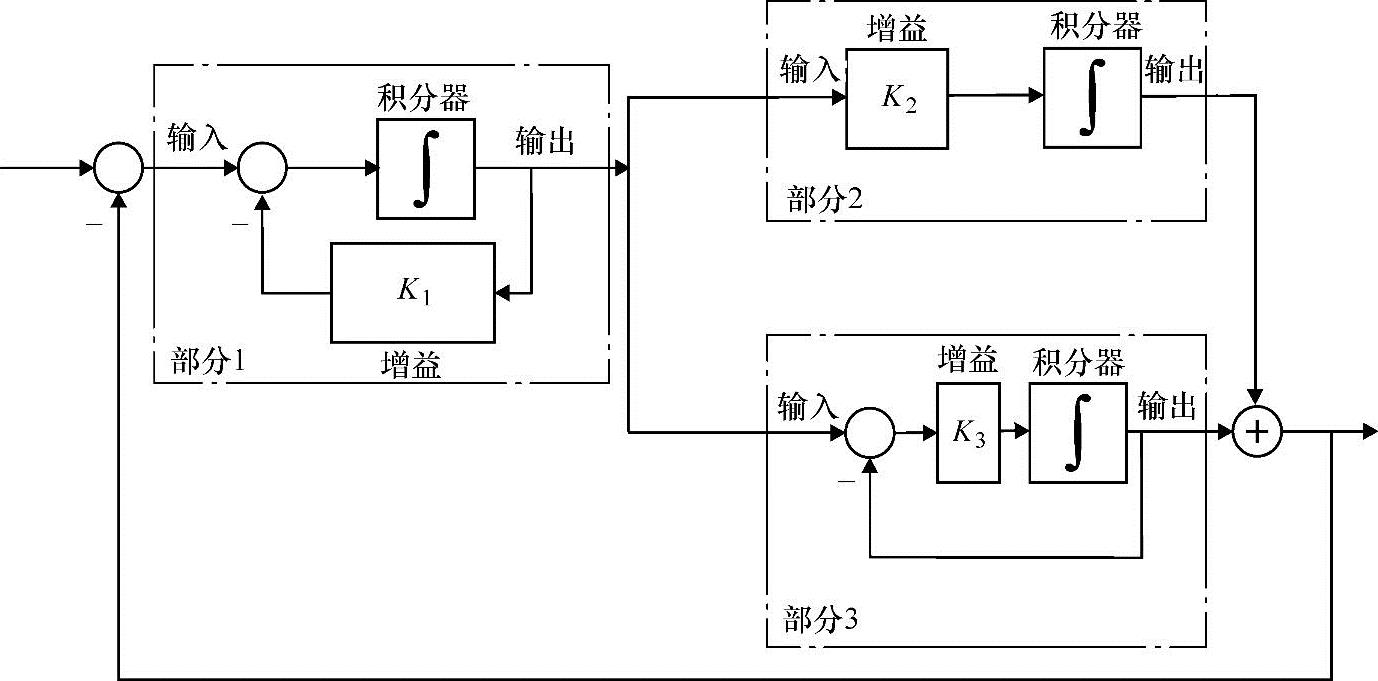
图5-9 表明组成结构和内部关系的系统结构图

图5-10 框图

化简1和3部分的反馈回路后，系统的内部结构如图5-9。部分2和3是并联的，它们的总传递函数是两者的和，将它们连接后的部分称为成为部分4。部分4的传递函数可写成E₄=E₂+E₃=K₂/s+K₃（s+K₃）-1。如图5-10所示，部分4与部分1串联，所以这个串联连接的传递函数是两者的乘积，

E₄E₁=（K₂/s）（s+K₁）-1+K₃（s+K₃）-1（s+K₁）-1

这些连接还都在一个反馈回路中，所以输入输出的传递函数是（1+E₄E₁）-1E₄E₁。通过一些代数知识，我们可知

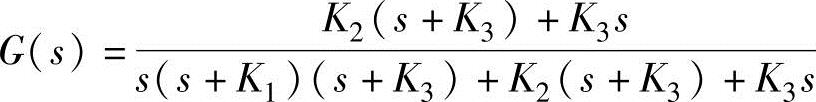
或者以s降幂排列成：

将s=jω，带入，就可得到频域响应。