黑盒子模型,一般也被称为输入输出模型,它表示系统中元件信号的处理方式。当我们讨论的是特殊的线性时不变系统时,这些元件也是线性的,而且能够利用框图知识快速地将它们与其他元件连接。
使用像我们在前面章节使用的积分器符号,连续的系统两种主要操作可表示如下:
(1)传递函数
考虑这样一个系统,系统的输入u(t)(拉普拉斯变换是u(s))和输出y(t)(拉普拉斯变换是y(s))(见4.3节),初始条件为0,输出的拉普拉斯变换和输入的拉普拉斯变换成比例关系。在复频域中,输入与输出之间的因子就是系统的表示符号:
y(s)=G(s)u(s)(5-8)
一般被称为系统传递函数,在框图中,我们通常在方框中填写G(s),从而代表系统[8]将输入乘以传递函数就可以得到输出(当然是在复频域)。
这说明了复频域的作用,时域的积分仅仅是频域的代数计算。
具体来说,对于积分器,如果我们将拉普拉斯变换的性质(见4.3节)用于式(5-4),可表示为(假设0初始条件):
微分用s表示,积分用s-1表示。积分与微分互逆。利用s表示微分的方法和方框图的变换规则非常有助于解释为什么线性系统的输入与输出之间可以用符号G(s)连接。(https://www.xing528.com)
(2)频域响应
当输入是正弦函数时,我们很想知道线性系统的输出是什么,即u(t)=U0sin(ωt),在稳态下输出[9]是与输入有相同的脉冲,不同幅值和相位的正弦函数,即y(t)=Y0sin(ωt+φ)。输入与输出的关系可以通过一个复数函数G(jω)表示,G(jω)的模和辐角为:
因此,对于任意一个ω1,G(jω1)使输出相对于输入的增益和相位发生变化。如果输入是正弦信号的指数形式,那么可以很容易得到G(jω1)。假定输入为[10]u(t)=Uejωt,系统的(稳态)输出为
符号G表示拉普拉斯变换,这表明传递函数与频率响应特性之间有特殊的关系,事实上是:
G(jω)=G(s)s=jω(5-11)传递函数运算符
在一个线性时不变系统中,传递函数运算符为线性系统提供了一种频域范围内的代数表示法。频域范围内的系统响应y是传递函数G(s)和系统输入u的乘积,即y=G(s)u。在正弦稳态情况下,输入为u(t)=Uejωt,则输出响应为y(t)=G(jω)Uejωt。通过例子,我们给出一个微分方程格式的过程模型:
假设零初始条件下,应用拉普拉斯变换的结果是:(s2+2s+10)y(s)=(s+5)u(s);或者表达为G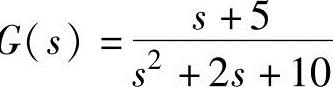
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




