积分器：如何实现低通特性

另外一种易理解且实际中常用于物理系统建模的模型就是积分器模型。在第2章中，我们知道积分主要的作用是保持和储存。一个简单的物理例子是水箱（或者厕所的水箱，如图1-2所示）。蓄水量表示输入水流和输出水流变化的总和。在这里，水箱的液面高度是一个重要变量。假如在时刻0时，我们开始向水箱注水，那么时刻t的液面高度取决于（0，t）时间段内输入输出水流量和初始液面的高度。所以，我们说水箱有记忆，这也称为水箱的状态。事实上水箱的容量有限，比空的还少或者比满的还多是不可能的。积分模型是这样水箱的抽象，它没有极限（它不能空也不能满）。水箱这个物理例子可以类比于电力工程中的电容，它的模型也是积分模型（电容是贮存电荷的容器）。水文学中的蓄水池或浴盆也可以建模成积分环节。热力学中的绝缘炉是热量存储。在以上这些例子中，输入分别是液体输入输出阀门的开度、电力供给和能够提供热量的冷热液体的热交换，输出则是水箱的液位、电容中存储的电荷、浴盆中的液体体积和绝缘炉中存储的热量。示意图如图5-4c所示，积分器的运算符表示如下：

从数学的完整角度，用微积分的知识将输出y，输入u和初始条件y₀写成积分器为

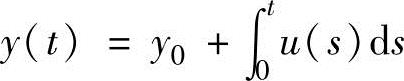
或者^[5]

后一个等式可以理解成输出的导数等于输入，或者输入的积分是输出（当然这也是前一个等式描述的思想）。为了使输出唯一，我们还在给定的时间点赋予输出一个值（这也称为输出信号的初始条件y₀）。使用微分的表达（等式5-4）非常有用，在为方便计算的仿真包中也是这样使用的。

积分器很显然是串联的，当前的输出和状态只取决于过去的输入。

积分器是时不变的。想想水箱的例子，无论是今天供水，还是明天或者昨天供水，供给水箱相同的水就会产生相同的水位变化。从方程中可以看出，只有信号本身，没有任何涉及时间的参数。

积分器也是线性的，如果（u₁，y₁），（u₂，y₂）都具有积分行为，那么对于任意的常数α，β，线性组合α（u₁，y₁）+β（u₂，y₂）也具有积分行为。又例如下面的例子（注意初始条件！）。

假设一个正弦输入u（t）=Asin（ωt），初始条件为y（0）=y₀，则

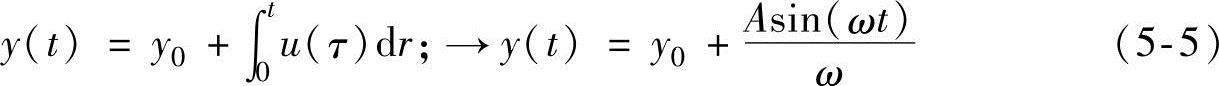(www.xing528.com)

含有积分器的系统具有以下性质：

1）积分器具有记忆功能，为了知道未来的输出，需要知道现在的输出和到将来输出的那段时间，而且积分器有初始条件。因此，当前的输出值充当积分器系统的一个状态变量。

2）积分器的零输入响应是一个常值信号。所以积分器可以看作是一个常值信号发生器。

3）积分器的常值输入响应是一个斜坡信号，所以零输入时，两个积分器串联可以看作一个斜坡信号发生器（见4.2.1节）。

4）积分器的响应由两部分组成：一部分是初始条件x（0）的响应，另一部分是输入的响应。

5）积分器在t时刻的响应是否已知取决于在t时刻以前（不包括t时刻）的输入是否已知。

6）积分器是线性的，时不变的，严格串联的系统。

7）让初始条件为0，或者说是只考虑由输入产生的响应。通过式（5-5）的正弦输入，我们可以知道：

①输出与输入的脉冲相同，这个性质对所有线性系统都适用。

②输出的幅值从A变为A/ω，输入变化的越快，ω就越大，响应的幅值就越小。我们称积分器拥有低通特性。如果输入的频率增加10倍，它的增益就会减小为原来的1/10，通常被表示为减小20dB^[6]。

③输出的相位从0变为-（π/2），称输出较输入滞后了90°或π/2弧度。