线性增益：简单系统的输出信号与输入信号成正比

线性增益可能是最简单的系统或模型：输出信号y就是由输入u和增益系数K简单地相乘，即y=Ku。

当输入信号是一个正弦波，输出信号就是一个同频率、同相位，但幅度不同的正弦波。输出幅度与输入幅度的商就是增益系数，如图5-4a所示。

很好的近似后用纯增益建模的物理系统的例子，是像杠杆、变速箱、电气系统中的音频放大器这类机械系统。

如图5-5所示的杠杆，我们测量的信号是杠杆每一端的位移，这里记为u和y。输入输出是什么很大程度取决于杠杆的用途。在这个程度上，行为的描述其实是无关紧要的。我们没有必要去决定哪个信号是输入，哪个信号是输出（事实上在这种情况下，我们无法作出区分）。在所有情况下，我们会发现，位移信号是互相成比例的。杠杆是线性的、时不变的、串联的，但是不满足严格串联关系的系统。用符号表示如图5-5所示，表达式是所有u，y信号的集合：

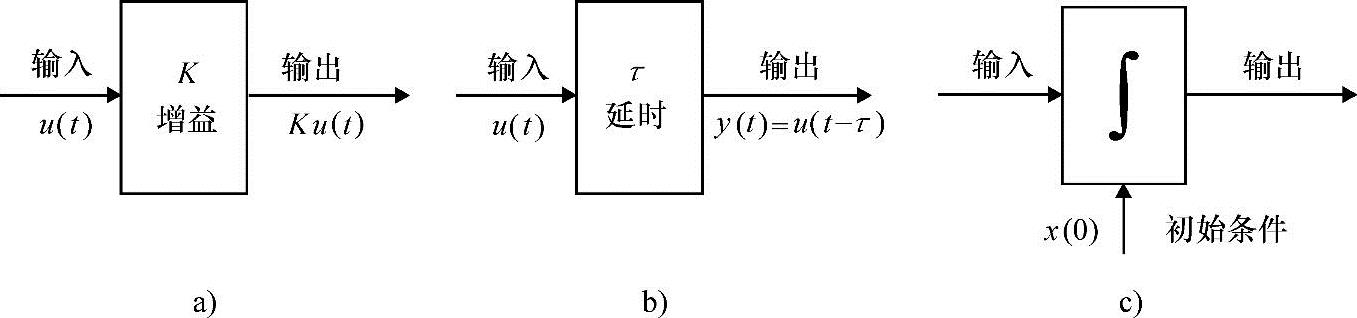
图5-4 基本系统

a）静态增益 b）纯滞后 c）积分器（累加器）

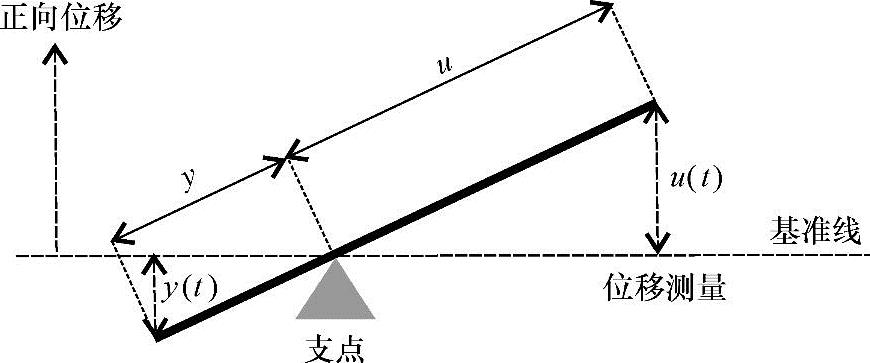
图5-5 杠杆，位移测量u，y

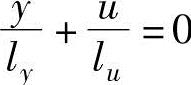(www.xing528.com)

式中，l_y，lu是杠杆臂的长度，从支点到每一端分别测量。

当杠杆的一端作为驱动，称作u端；另一端就作为负载，称为y端，这样就清楚了杠杆的哪一端应该是输入，哪一端是输出。

其他与杠杆有关的测量或信号是力。结合力和杠杆，可以考虑应用动量或其他知识建立一个杠杆运动的动态模型纯增益系统不具有记忆功能。在这种情况下，输出等于输入乘以增益，所以我们需要凭借未来输入预测未来的输出。在这种情况下是没有状态变量。

例如：变速箱的输入可以是输入轴的转速（电动机从动轴），输出可以是输出轴的转速（负载侧）。另一种方法输入可能是在输入轴施加一个力或力矩，输出可以是输出轴位置，速度，或者输出轴的扭矩。同一个物理系统可能有很多相关的输入输出对，选择反映了我们的兴趣，在恰当位置安置更好的传感器，这是我们物理系统的组成部分。

音频放大器的输入是传声器或光盘产生的电信号，输出是声信号。这样一个系统不是一个被动的系统。在输入端到音频放大器的可用总（电）功率通常比输出端的（声音）功率少得多。事实上，这种情况下想用线性增益表示系统是因为我们对该系统的内部工作机制并不感兴趣。通常传感器或执行器就是这种情况，通常后者提供大功率、高的能量增益和增益信号。

当我们将传感器模拟为一个线性增益，这个增益必须与物理系统的输入单位和输出单位匹配。例如，在音频放大器中输入信号单位通常是电压（伏特），声音信号单位是声压（帕斯卡）。

实际上没有系统是一个简单的线性增益。系统总会有操作时的物理限制。杠杆受力过大就会弯曲；扬声器的声音信号功率过大或频率过高，扬声器就会饱和以致变声；其他的影响、可能发生在信号非常小的时候。在齿轮传动系统中，当改变齿轮的旋转方向时，输出响应滞后于输入（见3.4节）。如果输入力矩不能克服摩擦力和齿轮传动链的静摩擦，齿轮根本不会转动。因为这些影响是重要的，他们当然应该成为模型的一部分。当我们将一个特定的系统考虑成线性模型，这表明假设系统/模型的信号没有那些复杂的情况。

线性系统具有两个重要的特性：立即性（无记忆）和线性。