记录和重放在不同信号环境中的应用

很显然，实际的世界并不是数字的，有很多的信号本身是非数字的，就像音乐一样。我们为了可以用数字化的方法存储音乐，就需要建立从模拟世界到数字世界和从数字世界到模拟世界的连接系统。

其主要思想是我们需要使用一系列基本函数，比如与频率协调相关的正弦曲线来表示一个可测的信号。这种表示方法的经济性和处理测量误差的能力，解释了它的效用，就如同上面例子中解释的那样。在不同的信号环境中，需要选择不同的基本函数集合，但是其基本思想却是一致的。这里有一种有趣的折中办法。通过丰富基本函数集合，我们显然可以建立更多的模型，但是同时检测错误也会随之增加，因此我们更倾向于灵敏度而不是误差率。使用的函数越少，就越不易建模，但同时错误会减少。从科学的观点来看，我们倾向于后一种方法。

举个例子，当信号为脉冲信号时（大多时间为0，在极端的时间内产生峰值），正弦函数族不宜作为建模的函数类。如图4-17所示。

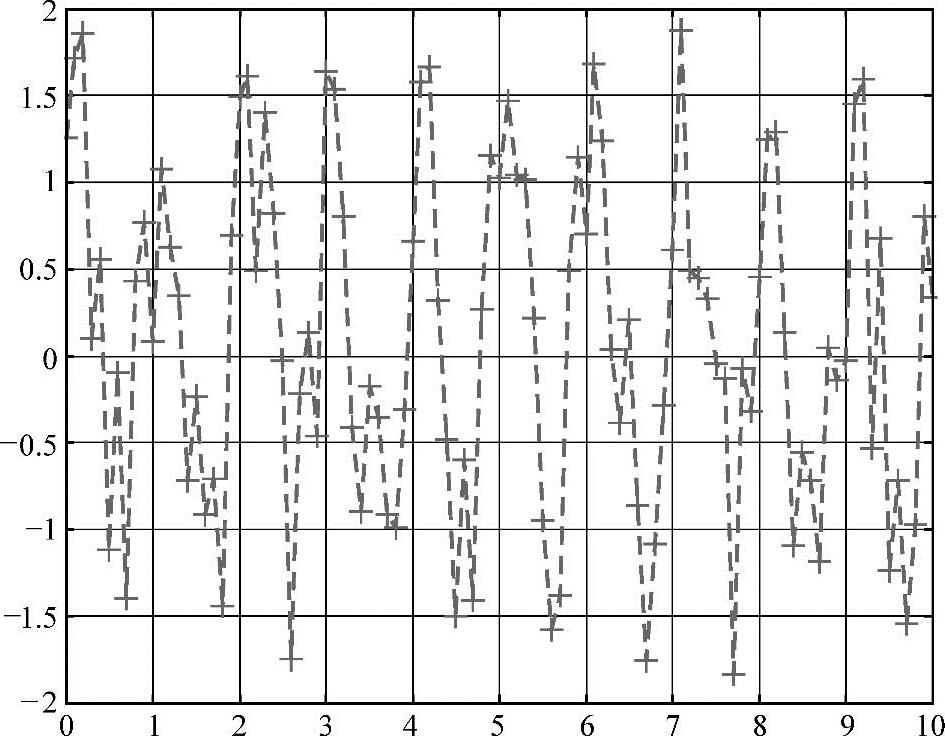
图4-17 正弦函数sin（2πt）在区间为（-1，1），T_s=0.1的抽样周期内收到随机噪声影响的图像

（这类信号常用来建立大脑神经活动的模型）这类信号频谱很广，并且从结果可以看出时域信号的表示方法比频域信号更紧凑。这种现象是与傅里叶变换（见图4-18）相关的不确定性原则的表现：当信号能量位于时域内一个较小子集时，它的频谱将占有频域中的较大子集（或者信号能量在时域内分布较大但在频域内占有率较小的情况），这种情况如图4-19所示。(www.xing528.com)

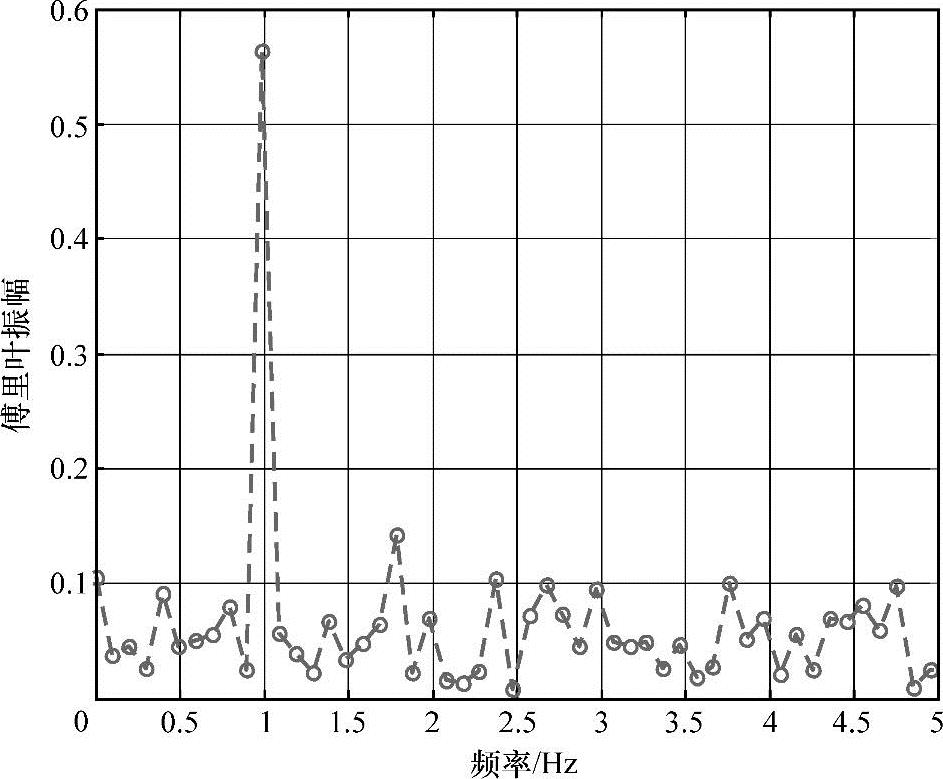
图4-18 此为图4-17信号的在周期确定时的傅里叶变换族

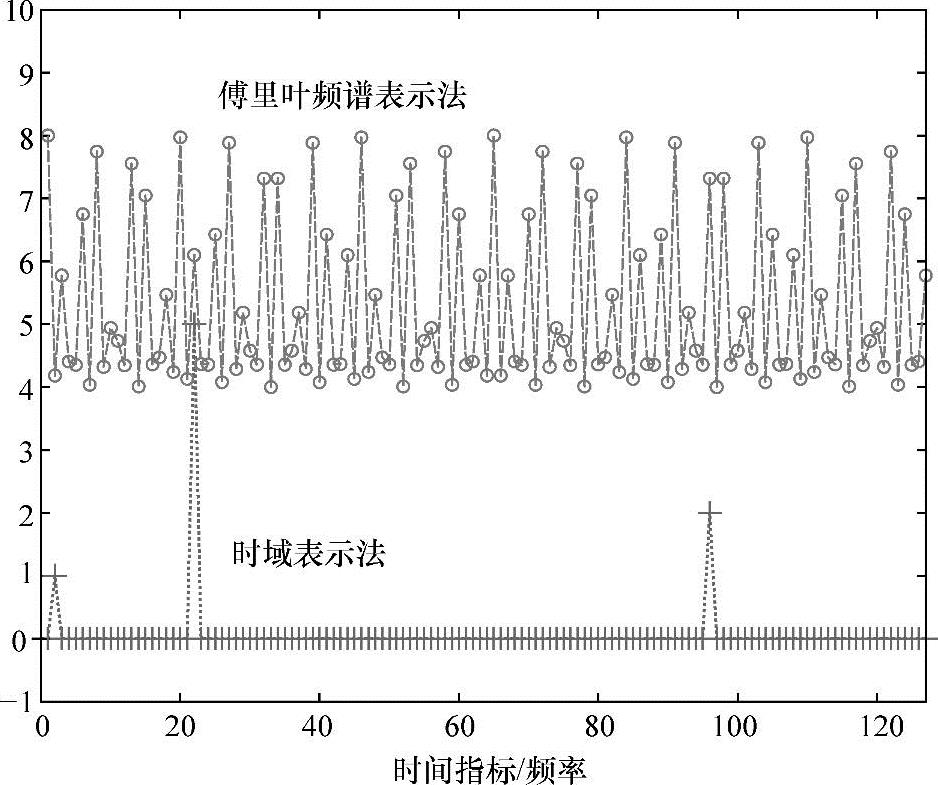
图4-19 尖峰信号的宽频波谱（128个取样点，128次傅里叶变换）