重新看图4-12,可以表示为y=M(u,d),在测量系统输出值y和感兴趣的值,即测量系统输入信号u之间总是存在误差。信号处理与信号理解有关,特别与信号恢复有关,即那些需要测量的信号。换句话说,信号处理感兴趣的是,我们是否能找到另一个系统SP,作用于信号y并恢复信号u,例如,信号SP(y)-u或者等效的SP(M(u,d))-u在适当的方式下很小。
测量过程通过M的信息决定u,或者是干扰d的一些信息,当然给定测量量y通常是很难的,甚至是一个病态的问题。
把问题变得更易于处理的一个方法是在输入端口添加结构。例如,假设u是二值数,假设在任意时刻u(t)=1或-1,这使问题在很大程度上得到了简化,允许我们抵制噪声和不好的测量结果。这可以成功地做到,并可以很好地解释为什么我们生活在一个信息以数字格式进行存储和交换的世界里。在自然世界中也是这样的,事实上,生命程序用DNA进行编码,使用了4个字符的字母表。尽管存在很多生物学过程的随机性,以DNA编码的生命程序的复制、遗传和执行,拥有很高的精度,从今天生命依然存在的事实来看,这是显而易见的。
编码和压缩:
通过琐碎的插图,假设u(t)∈{-1,1}是二值的。让测量过程仅仅加上噪声n。因此y=u+n。只要噪声是有界的,例如n(t)<1,只要选择输出y的符号就能恢复信号u;u=sign(y)=sign(u+n),如图4-16所示。
在图4-16中,测量误差被限制在0.95。十字代表原始信号,圆圈代表恢复信号,点代表测量信号。
在工程中,处理二值信号是数字信号处理的主题。当处理关于复杂二值信号的问题时,我们利用Claude Shannon在他1948年发表的著名论文中的信息理论。复杂的理论处理这样的问题:这里有多少个不同的信号。问题的前提条件是信号只能通过有限精度容量的测量过程得到。在这种情况下,自然会对两个特定的问题感兴趣:(https://www.xing528.com)
1)怎样保护一个数字信号不受其他信号的干扰。
2)怎样使信号信息的丢失变得最小,在必须要减少信号表示的时候,例如当没有足够的空间去存储和转换信号时。
第一个问题可以通过编码的方法处理。编码是构建冗余的信号进行存储、检索和交换。冗余量,通过一种标准的方法获得,有助于对抗噪声。许多可能发生在检测或传输过程中的错误可以利用已知的冗余信号进行消除。
第二个问题属于压缩方法的范畴。通过有意减少表示一个信号的比特数,基本信息可以尽可能的保留。通常利用信号中的自然冗余可以减小信号的长度,这种方法称为无损压缩。无损压缩通常不能实现位长的大幅度压缩,不过这个问题可以解决。另一方面有损压缩方法可以显著的减小信号的长度,但是不能这么操作:信息会丢失。
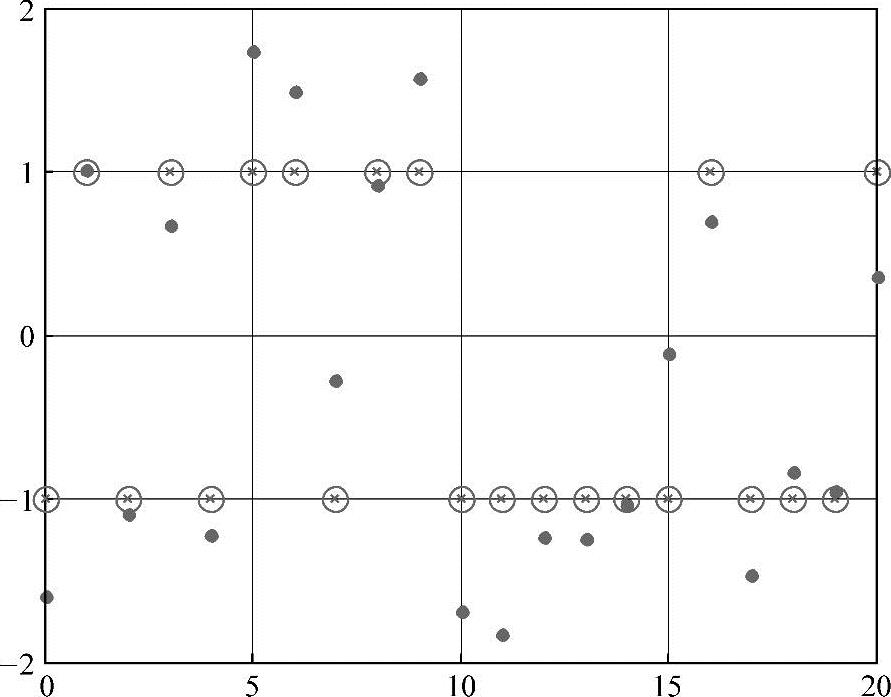
图4-16 从噪声中恢复的二进制信号
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




