解决混淆问题：周期信号采样

若考虑对一个周期信号进行采样会发生什么？假设采样过程是理想的，采样没有延迟，无限精度。考虑采集到的是等距样本，样本时刻t_k=kT_s，k为整数，正数T_s>0为采样间隔。对正弦信号式（4-5）进行采样，s（t）=hsin（ωt+φ），得到测量信号s_s

s_s（k）=s（kT_s）=hsin（ωkT_s+φ） k=0，1，…（4-14）

以采样周期T_s进行采样，采样周期与信号周期有s着理性的关联，于是产生了离散时间周期信号s_s，而且存在整数K使得s_s（k）=s（kT_s）对于所有的整数k都是成立的，下面就是这种情况，当下式为一个合理的数。

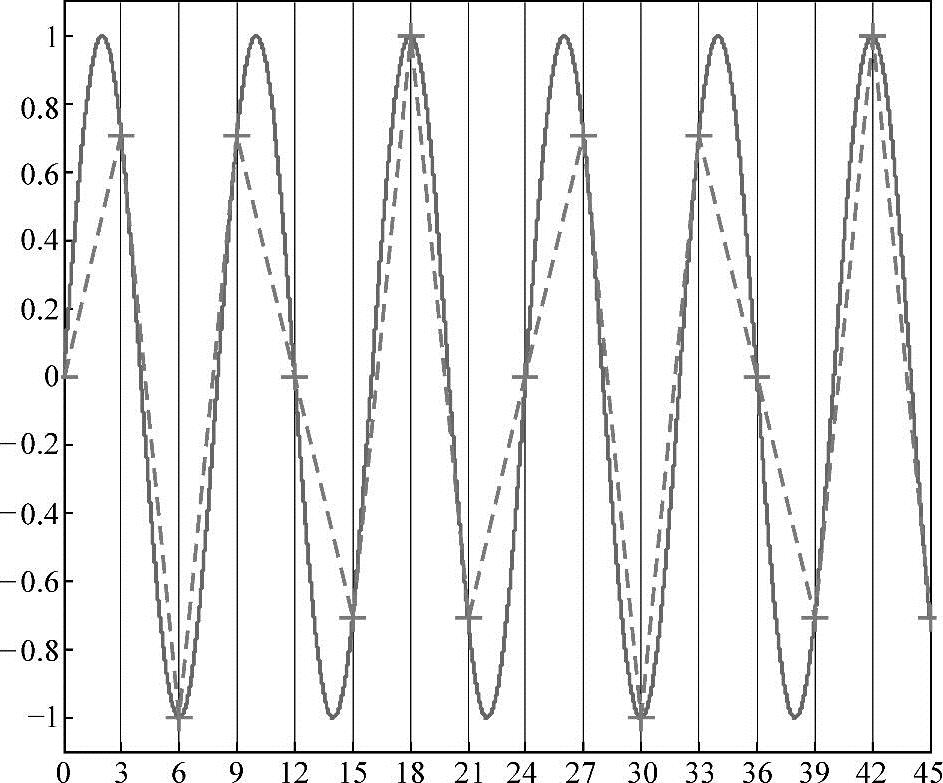
采样信号时间单位的周期是KT_s。至少要和信号本身的周期一样大，即KT_s≥T，例子如图4-14所示。

对于T_s=T，我们实际得到的s_s是一个常信号！这种现象称之为量化噪声。通过令2T_s<T可以消除量化噪声，或者令采样频率f_s=1/T_s至少是我们想要采样的信号的频率的两倍。如图4-14所示中的采样满足了这种标准。这个基本的观察源于奈奎斯特和香农。当以常采样频率对特定信号（不必是周期信号）进行采样时，这具有很强的普遍性，同时采样频率必须至少是信号频谱中最大频率的两倍，以消除量化噪声。由于量化噪声造成的显著的信息丢失的本质（见图4-15）说明。

(www.xing528.com)

图4-14 以3为采样周期对周期为8的正弦连续时间信号采样，产生一个周期为24的周期性离散时间信号

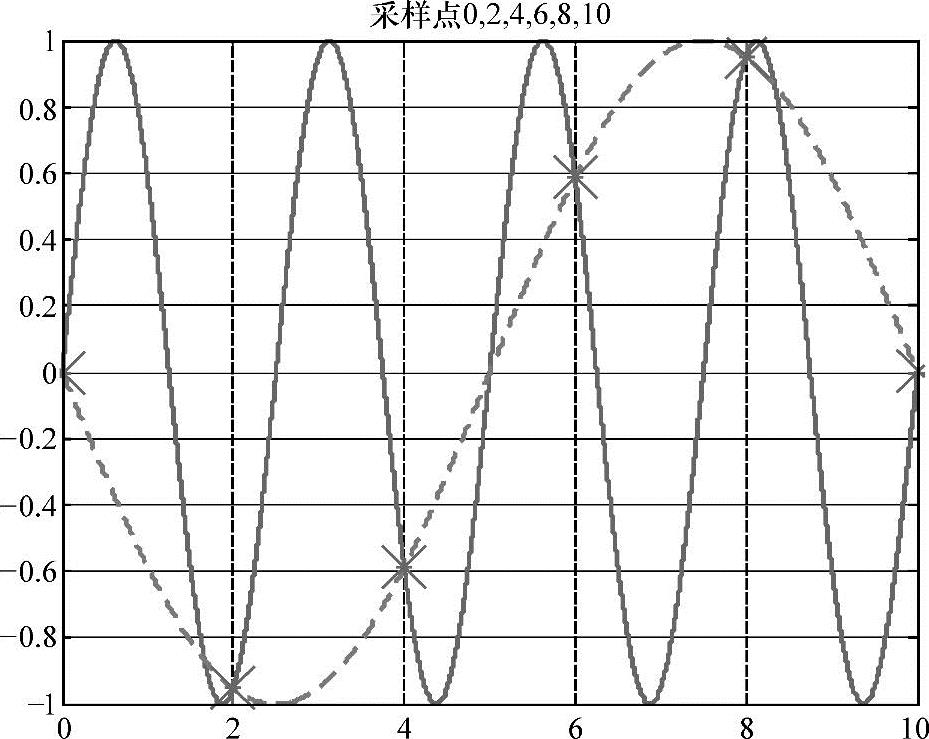
图4-15 频率为f₁=0.4Hz的正弦函数sin（2πf₁t）和频率为f₂=0.1Hz的正弦函数-sin（2πf₂t）当采样频率为0.5Hz产生相同的抽样数据序列

量化噪声可以通过两种方法来避免。一种是确保将要测量的信号是足够缓慢的，另一种是对将要采样的信号进行预处理，消除能够引起量化噪声的快信号变化。这需要所谓的抗混叠滤波器。信号的周期采样：奈奎斯特-香农定理

无信息损失的对信号进行周期采样要求采样频率等于信号谱内容中最大频率的二倍。实际中抗混叠滤波器加强了这一条件。滤波器确保了频率为f_s的采样信号的谱内容低于0.5f_s。