周期性信号及其性质

老爷钟摆动臂或节拍器（见图4-7）是周期性摆动的。如同设计的那样，它可测量摆钟极限位置之间的等时间间隔。作为演示，这个摆的角度以时间为轴绘于如图4-8所示。显然有一部分图片是重复的，称角度是一个周期性的信号。

信号s被称为周期性，存在时间间隔T，信号每隔T个时间单位变化一次，在任意t时刻，s（t）=s（t+T）。满足上式属性的最小的时间间隔称为周期。

周期现象是很普遍的，在我们现代社会中，根据周期性现象，我们选择组织我们的生活。我们习惯于年度、季节性和日常模式。在生物学中，心率、呼吸节奏和激素周期都扮演重要的角色。它们并不是真正的周期性而是近似有周期规律（事实上固定周期往往表明错误的事情）。在工程系统中，周期性的运动无处不在，因为它结构简单。一个电动机或发电机的轴，一个气缸在内燃机的位置，一个变速箱的角位置，光盘播放器的阅读位置或录音机都具有周期性信号。同时乐器奏出的音调、交通信号灯和火车时刻表都是周期性信号或可以建模为周期信号。

图4-7 节拍器，用来提供一个时间的参考

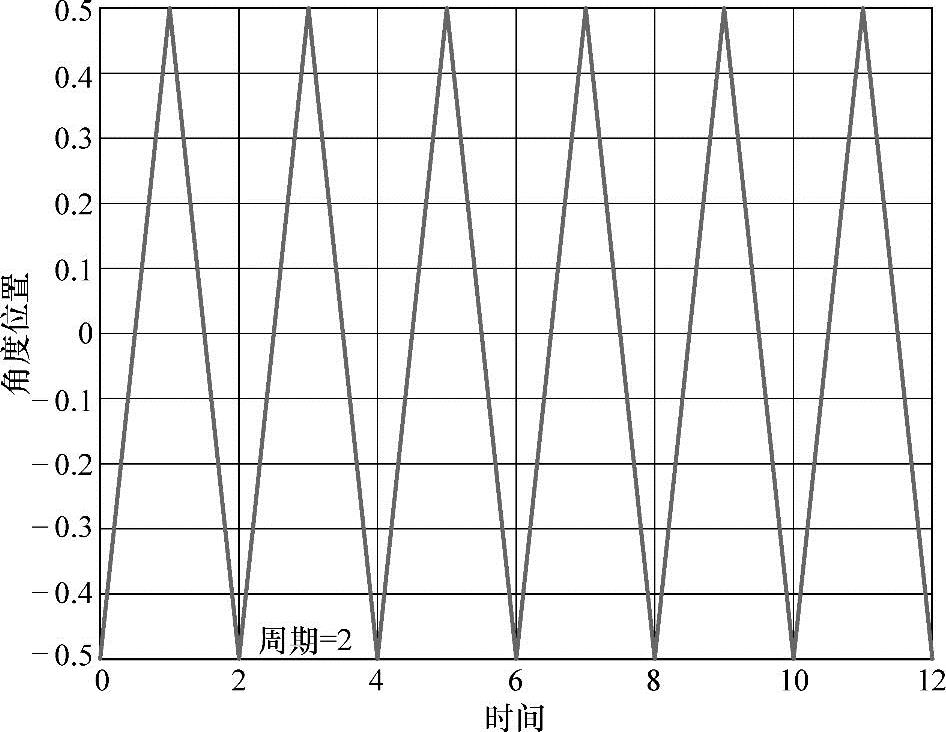
图4-8 绘制节拍器的角度-时间曲线，所谓的（周期性）锯齿波函数

一部分特定的周期函数（见图4-9），原则上，时间轴必须无限期地延长（包括向前和向后的时间），但我们当然不能在一个图中表示。

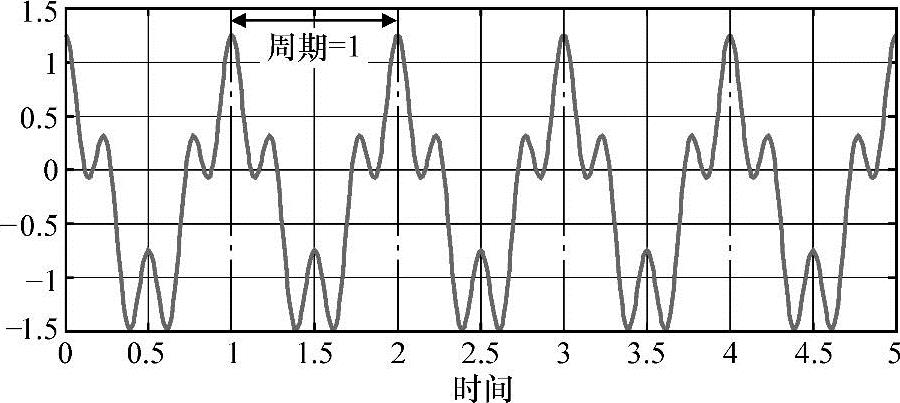
图4-9 一个周期为1的周期信号(www.xing528.com)

一个周期性信号是确定的和可预测的。的确，观察周期信号通过一个时间周期内的信号（这里无所谓观察到哪一个时间周期）足够来预测它在任何未来时刻（在将来）的值或重建它在任意过去时刻的值。所有周期信号都是确定的，但并不是所有的确定性信号都是周期性的。

而且几乎所有周期为T的周期信号都可以表示为正弦信号的集合（见式4-5）：

1/T被称为基本频率，为谐波的倍数。这样的表达式称为傅里叶级数。这个概念如图4-10所示。

周期为2π的不连续波相继地被其基波和3次谐波近似。注意到其近似值是连续周期函数。因此，我们必须小心解释，这种近似确实接近所关注的函数，且当包含更多谐波函数时更接近^[10]。

适当的正弦信号的总和可以用来近似任意信号。这类信号有巨大的灵活性。对于几乎任何信号s（t），有可能找到一个适当的振幅、频率与相位的集合以正弦曲线之和来近似s（t）。观察到尽管在这个集合中的每个部分都是一个周期性信号，但总和未必是周期性的。如果在这个和中有多限的信号，我们认为信号是准周期性的。一般，信号表示为一组具有任意脉动的正弦和，不是周期的，也称为非周期信号。

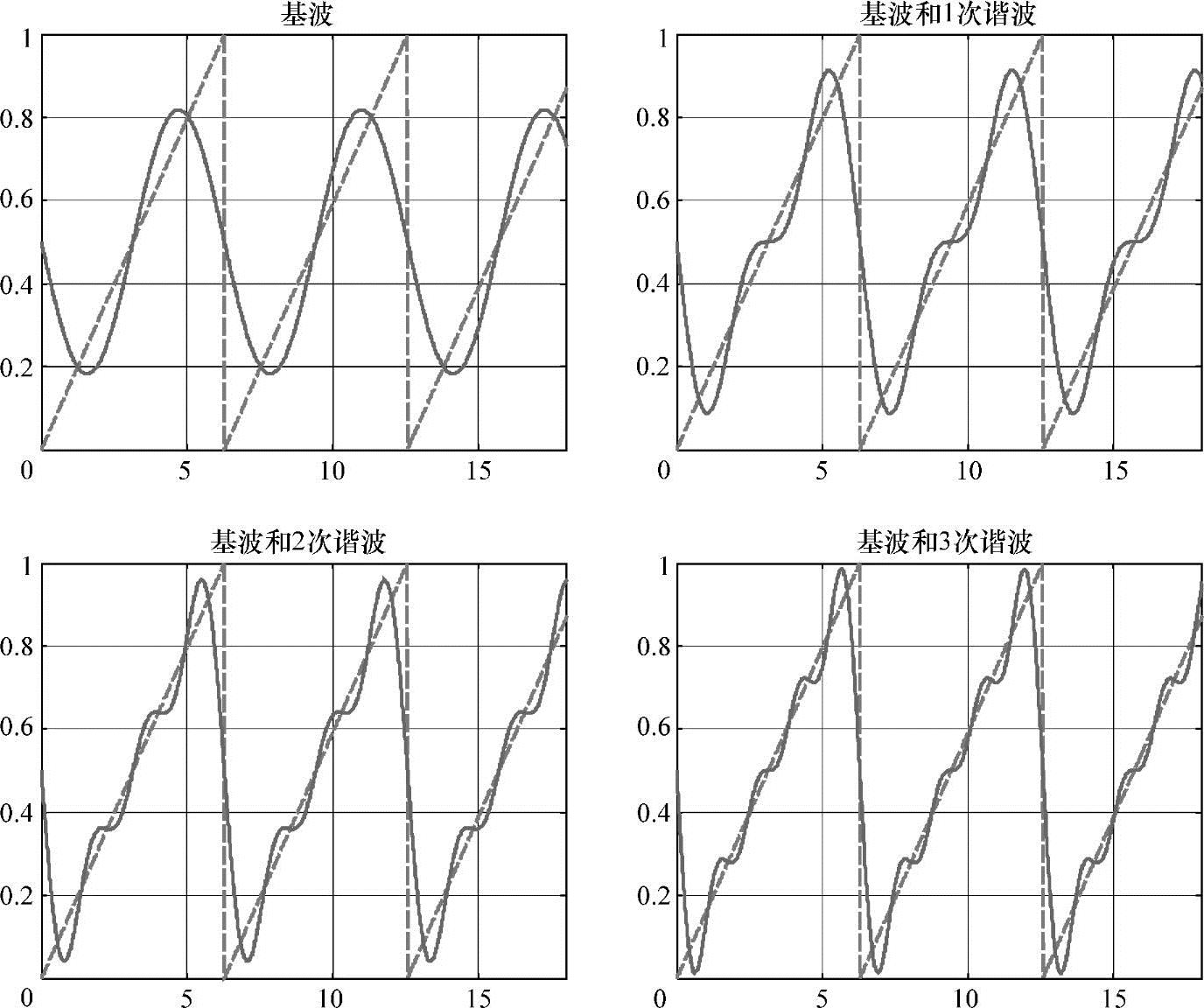
图4-10 一个周期信号，周期为2π。被前3次谐波无限接近