数学算法定义的信号简介

具有一个明确数学表示形式，并且在这个表示形式中我们能够可靠地计算信号值，这样的信号我们称之为确定信号。如图4-1所示中描绘的一些例子。

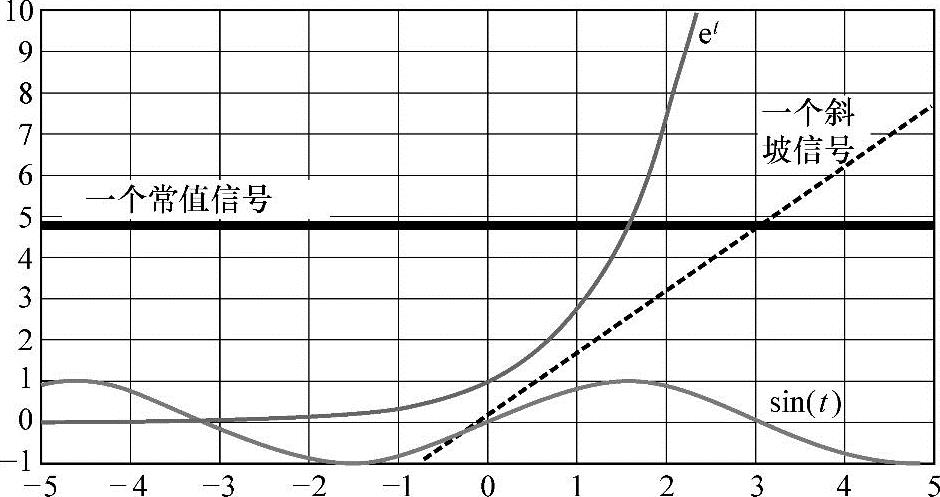
图4-1 在有限时间区间上表示的连续值域的一些简单信号

1.常值信号

常值信号被定义为s（t）=a，其中a是一个常数，不随自变量t的变化而变化。这是一个很单调的信号。比如，光速就是一个常值信号。由于其不随时间而变化，因此它的导数值（对时间的）是0，可以表示如下：

或

在系统语言中，我们可以将上述等式解释为常量信号是以一个零输入（即一个系统）和一个初值为常数积分的输出来进行建模的。

2.多项式信号

多项式信号是一个带有时间整数次幂的有限线性组合t，t²，t³，…，包括t⁰=1。它的形式是s（t）=a₀+a₁t+…+a^n-1t^n-1+a_ntⁿ，标量a_ii=1，2，…，n。如果a_n≠0，这样的多项式是n阶多项式，因为n是表达式中时间的最高次幂。

例如信号s（t）=1+t-t²+t³就是一个立方多项式信号，或一个3阶多项式。

一个常数信号，s（t）=a，a为标量，不受时间影响，这是多项式信号的一个特例。多项式的重要性可以从式中得知，即任何信号（在一些有限的时间间隔）可以由多项式信号任意近似。这是一个有用的属性，例如，从它的样本中能够插入或推断信号。这个结果是由Weierstrass^[4]证实的。

斜坡信号是一阶多项式信号的形式s（t）=at+b，a、b是标量。斜坡信号可以代表远程通信网络中的玻璃纤维中的光子位置，或者是常规角速度下的转角位置。斜坡信号的导数是一个常数信号。事实上，如果s（t）=at+b，它的导数是

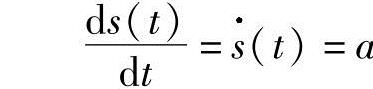
二次多项式，是形式为s（t）=at²+bt+c的信号（标量a，b，c）。它可以代表一个高尔夫球的轨迹，或导弹弹道（如箭）的轨迹。而且，它的导数是一个斜坡信号而其二阶导数是一个常量信号

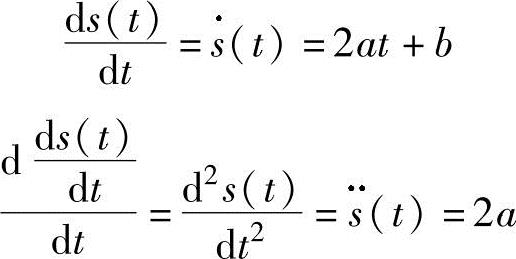
一个简单的，可表示任意3阶或更低阶多项式的网络系统反映在图4-2中。

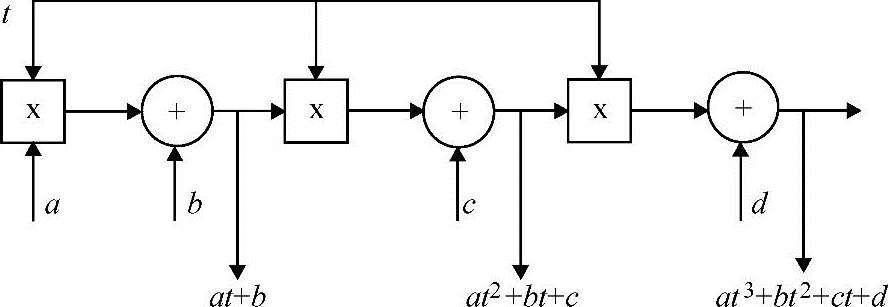
图4-2 一个可以计算任意不高于3阶的多项式信号的系统网络。网络的外部输入是信号t， 常数信号a，b，c，d是多项式信号的系数。网络计算了许多不同的从1阶到3阶的 多项式信号。这些信号被确认为网络的输出

网络只包含加法器和乘法器两个不同的系统，以线性方式从左到右安排，加法器后面跟着一个乘法器，如此交替排列。除了左边第一个乘法器外，乘法器接收两个输入，即即时时间（估计这一时刻的多项式信号）和它左边加法器输出。第一个乘法器接收首系数和即时时间作为输入。加法器也收到两个输入：一个被评估的多项式系数和左边乘法器的输出。很容易看到如何构建一个网络来计算所有任意阶多项式，它包含乘法器和加法器的数目和多项式的阶数一样。

另一种获得多项式信号的方法是使用级联，或者带有初值的积分器的串联结构。如图4-3所示。前一系统的优点是输入都是常量。

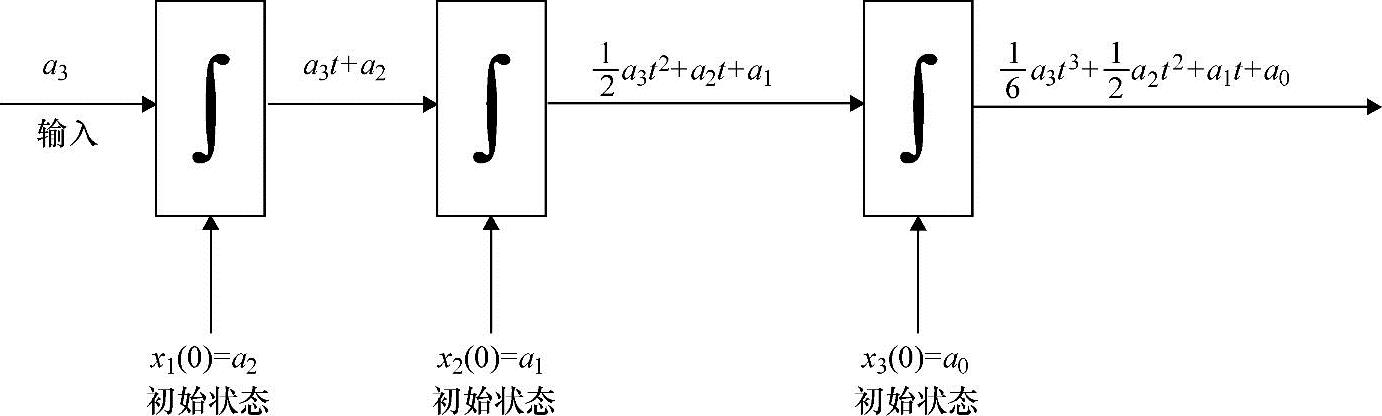
图4-3 3个积分器的串联能够计算任意不高于三阶的多项式信号

指数和正弦信号

指数信号的形式s（t）=be^at，a，b是标量，e是一个正标量^[5]，很容易理解，随着时间的推移，如果a>0，信号值将会增长，如果a<0，它将减少到零，虽然这需要耗费无穷的时间去衰减。这种变化被称为指数衰减到零。

指数信号可以被定义为那些和它们导数成比例的信号：

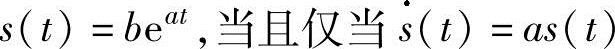
这个属性在信号分析中将会非常有用，因为任何时刻我们都会遇到如下形式的方程

然后，它意味着y（t）是指数，即解决式（4-3）的方案是一个指数函数。(www.xing528.com)

信号形如s（t）=hsin（2πt/T+φ）被称为正弦信号。我们已经看到这些种类的振动信号如图2-12所示，当一个无摩擦的质量-弹簧系统。这个信号的定义中含3个参数：振幅h，周期T和相位φ。这是一个周期信号的基本类型。

指数、正弦信号是一个指数信号和一个正弦信号的线性组合的结果，这样的信号在线性系统研究中特别重要。

同时，指数和正弦信号是密切相关的。在e^at中标量a为复数a=jω，其中，ω是实数，j是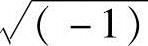）的表示符号，然后信号实际上成为了一个复杂的正弦信号，即e^jωt=cos（ωt）+jsin（ωt）（这种关系是欧拉发现的）。其中j²=-1从上面的关系，可以明显推论：

e^jπ=-1复数

一个复数是由两部分组成，实部和虚部，通常写成z=a+jb。这里j代表虚部的表示单位。

它有j²=-1的性质。a称为实部而b是复数z的虚部。复数可以被看作对应平面上的点。

一个复数可以用其模和相位表示，定义为

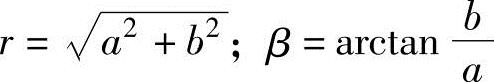
分别地r=e^α，e^jβ=cos（β）+jsin（β）

任意复数可以被写成a+jb=e^α+jβ（4-4）

两复数相加，其实部与虚部分别相加（a+jb）+（c+jd）=（a+c）+j（b+d）

两复数相乘，依下式：（a+jb）（c+jd）=（ac-bd）+j（bc+ad）

其中j²=-1

从上面的关系，可以明显推论：

e^jπ=-1

例如放射性衰变的建模要使用指数信号，因为事实上放射性物质含量的变化与可用材料成正比。因此，它可以建模如式（4-3）。

钟摆的摆动臂建模则使用正弦信号。如果没有摩擦，将观察到一个标准的正弦信号。在存在摩擦时，响应将是一个振幅依指数衰减的正弦曲线。这个过程如图4-4所示，这与如图2-13所示中的质量弹簧系统的阻尼振动相类似。

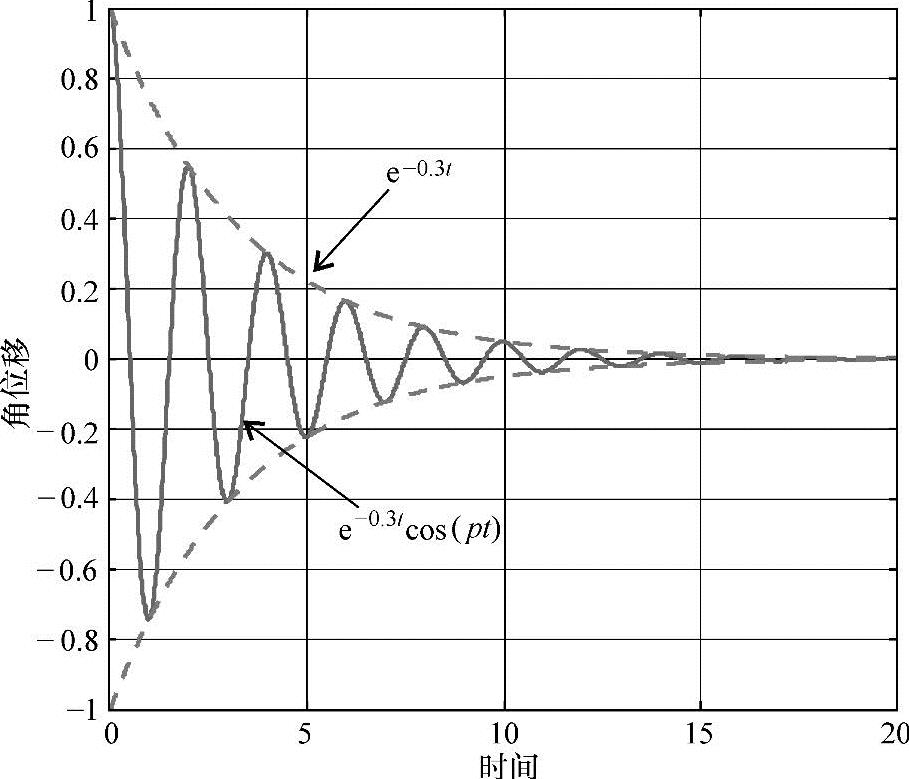
图4-4 受摩擦的钟摆摆动角度

正弦形式，一类特别的时间函数，特别适合描述周期性的现象。为了说明一个正弦曲线是什么，以及它是如何与线性系统密切相关的，我们精心设计。考虑仅有单个指针的一个时钟，假设指针以恒定的角速度旋转，则指针扫过的角度与流逝时间成正比。指针在圆轨迹上任意特定直径的正交投影长度定义了一个正弦信号。曲柄滑块机构如图4-5所示也是一个类似的情况，都是由圆周运动转换成水平轴上的前后运动^[6]。很明显线性位移信号是周期性的，因为指针的位置^[7]是一个时间和角位移的周期函数。

一个在常数角速度下的旋转运动导致正弦直线运动如图4-6所示。

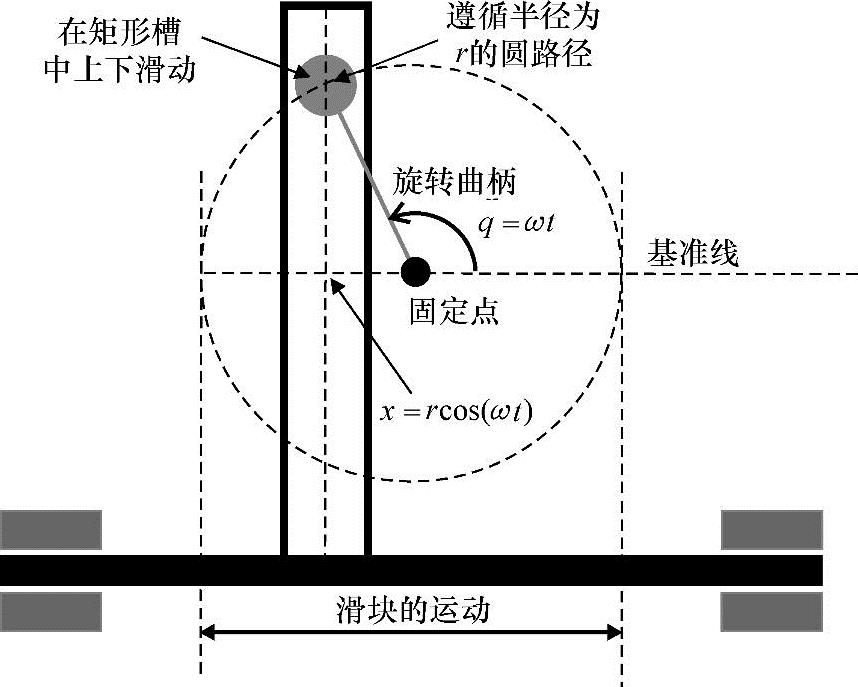
图4-5 曲柄滑块机构将一个旋转的运动变成一个特定的直线运动

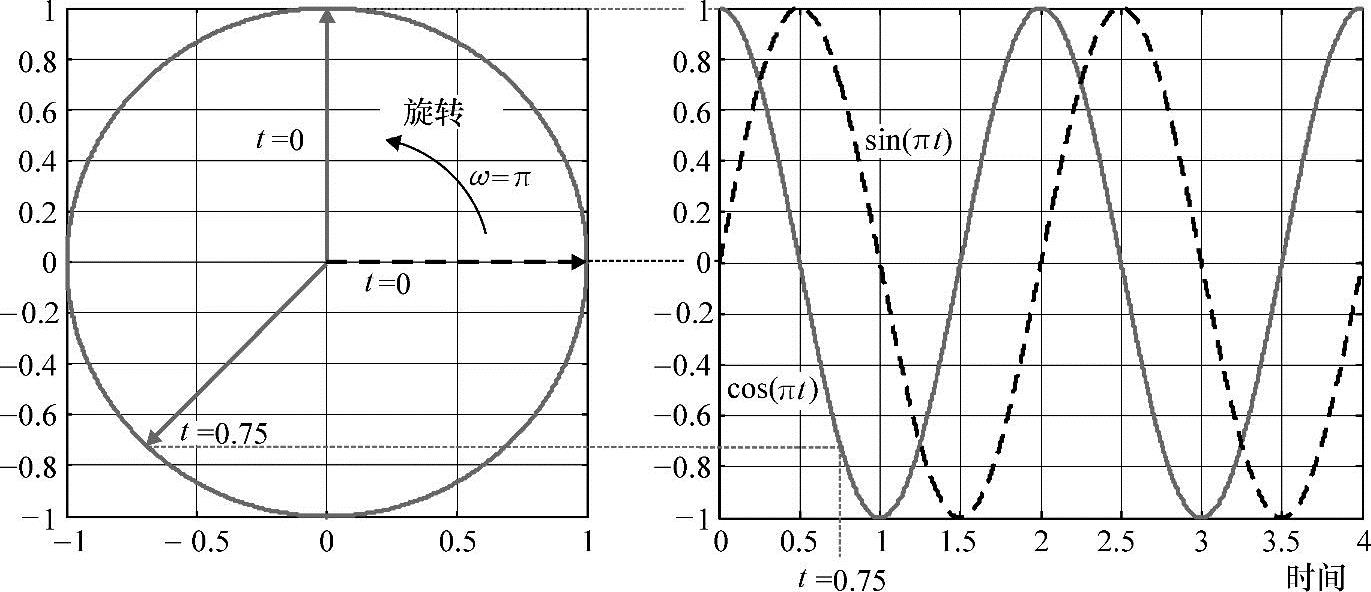
图4-6 匀速转动和正弦曲线是如何关联的

通常一个正弦连续时间信号表示为

s（t）=hsin（ωt+φ）（4-5）

单词“sin”是正弦函数sine的首字母缩写。t代表时间，单位为秒，以弧度表示的相角^[8]是φ，它被称为初始阶段的信号，且S₀是信号的最大值（量级）。相角确定参考时间。ω是正弦的脉动，被表示为rad/s（弧度每秒）单位下。h是振幅。

T=2π/ω是周期。频率是单位时间的数量值，v=1/T。频率的单位是赫兹^[9]，缩写为1Hz=s^-1。当φ=-π/2是余弦函数定义为cos（ωt）=sin（ωt-π/2）。