自校正控制系统优化方案

自校正控制系统是自适应控制系统中一个相当活跃的分支，它基本上从两个方面发展。一个是基于随机控制理论和最优控制理论的发展，最早是由卡尔曼（Kalman，1958）提出的，后来Peterka（1970）把自校正思想引入随机系统，Astrom和Wittenmark（1973）针对参数未知的定常系统正式提出“自校正调节器”（Self-Tuning Regulator，STR），把系统的在线辨识技术和最小方差控制相结合，构成了自校正的基本思想。Clark和Gawthrop（1975，1979）推广了Astrom的思想，在一般最优指标下给出适应控制——“自校正控制器”（Self-Tuning Controller，STC）。自校正控制系统另一方面发展是基于极点或极、零点配置理论的自校正控制。

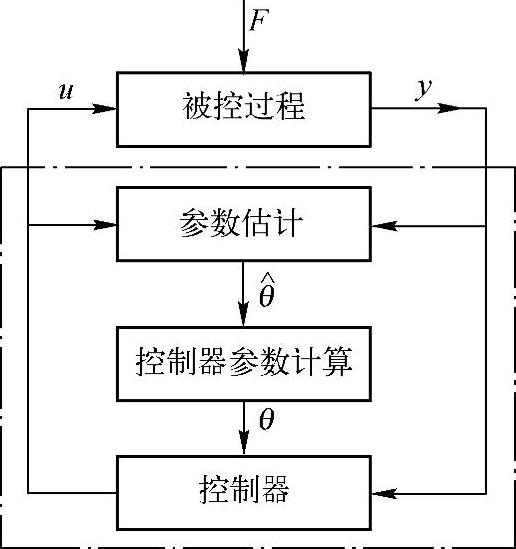
图2-26 自校正调节器框图

自校正调节器是典型的辨识与控制的结合体，其框图如图2-26所示。

辨识部分采用最小二乘法，依据过程的输入输出数据，得到数学模型的各个参数

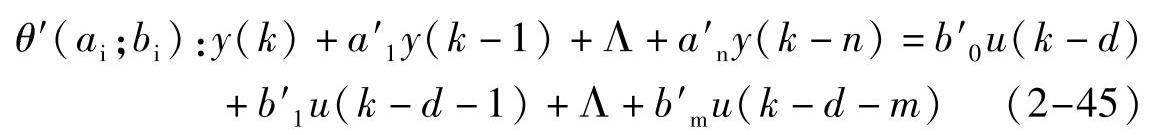(www.xing528.com)

式中，y为输出变量；u为控制变量；d为以采样周期表示的时滞数值。

控制部分采用最小方差控制。目标是求u使J=E[y²（k+1）]达到最小。首先是按参数已知情况下求控制律，然后用参数的估计值代替未知参数，如果参数估计是随着系统的变化而实时进行的，那么系统就是自校正的。

实践上，自校正调节器在国内外不少场合取得了成功，并且也出现了工业产品，例如ABB公司的Novatune自校正调节器。

自校正调节器还有一些问题，如：过程趋向平稳后，辨识与控制的矛盾会出现，并趋向尖锐。此时控制器对系统不再有充分的激励，辨识算法的进行遇到困难。对此Astrom认为应该在系统开始投入运行时辨识，到接近平稳时则宜暂停，隔一段时间再进行辨识。另外由算法得到的控制作用u（k）会大起大落，因为在目标函数中未考虑u（k）的平稳程度。由Clarke提出的自校正控制器，在目标函数中考虑了u（k），与线性二次型最优控制的做法相似，这样即可克服上述缺点。