模型参考型自适应控制系统简介

典型的模型参考型自适应控制系统如图2-25所示。图中参考模型表示了控制系统的性能要求。输入r（t）一方面送到控制器，产生控制作用，对过程进行控制，使系统的输出为y（t）；另一方面，r（t）送往参考模型，其输出为y_m（t），体现了预期的品质要求。把y（t）和y_m（t）进行比较，偏差送往自适应机构，进而改变控制器参数，使y（t）能更好地接近y_m（t）。

设计控制规律的方法主要有三种：

1.参数最优化方法

参数最优化方法利用最优化技术搜索到一组控制器的参数，使某个性能指标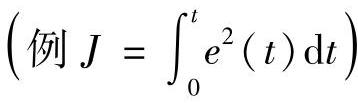达到最小，其优化的方法常用梯度法。这种设计方法的主要缺点是系统可能不稳定。

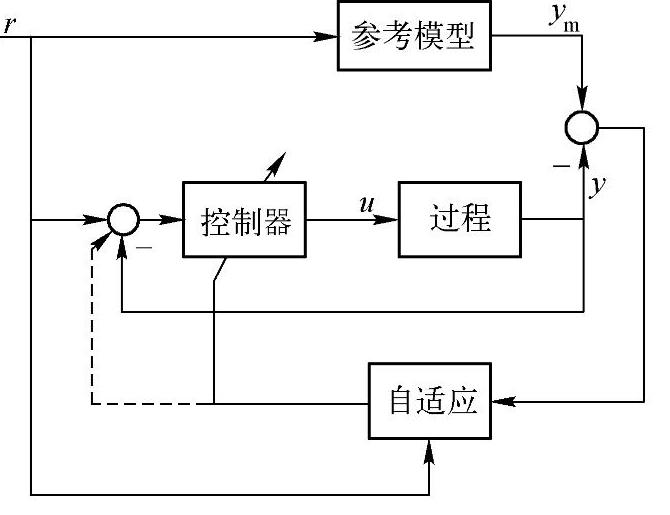
图2-25 模型参考型自适应控制系统(www.xing528.com)

2.基于李雅普诺夫稳定性理论的方法

这种方法的基本思想是保证闭环系统是稳定的，使广义误差e（t）趋向于零，用这种方法设计的系统一定是稳定的。但对于一个实际系统而言，仅仅稳定是不够的，还要考虑偏差e（t）趋向于零的速度，另外求李雅普诺夫函数也是一个困难问题。

3.利用超稳定性来设计自适应控制系统的方法

首先把系统变成等价的非线性时变反馈控制系统，即系统由一个线性前向环节和非线性反馈环节构成，前向环节应是线性的，且是正定的。反馈环节是非线性时变的，满足波波夫积分不等式，由此解出自适应控制规律。

模型参考型自适应控制方法的应用关键是如何将一类实际问题转化为模型参考型自适应的问题。