观测补偿器控制方案优化

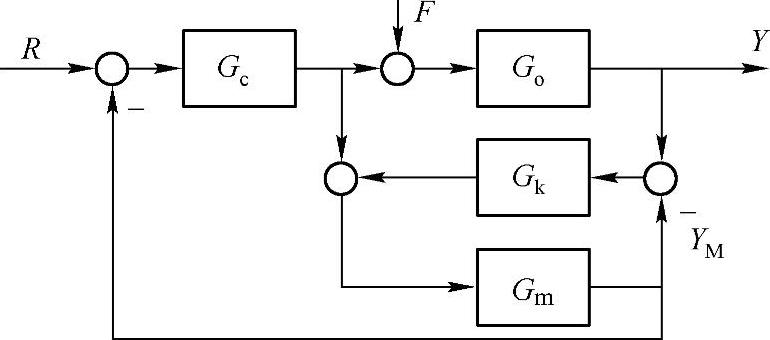
图2-21 观测补偿器控制方案

观测补偿器控制方案如图2-21所示，由图可得

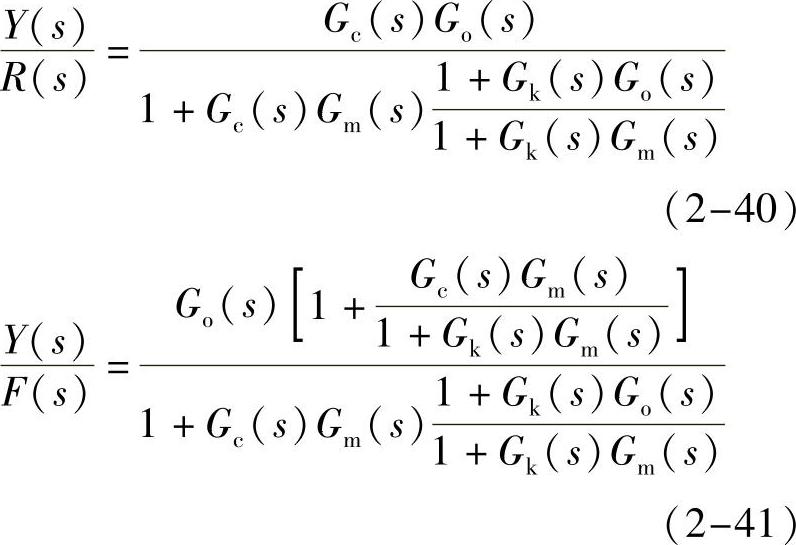
闭环特征方程可由式（2-42）求得

不管对象的时滞有多大，只要G_k（s）的模足够小，就有(www.xing528.com)

从而闭环特征方程成为

1+G_c（s）G_m（s）=0 （2-44）

系统的稳定性只与观测器G_m（s）有关，而与时滞大小无关。如G_m（s）=G_p（s），则式（2-40）与史密斯预估补偿控制的式（2-36）相同，表明其控制效果与史密斯预估补偿控制的相同。但本方案对于对象参数的变化不敏感，且不需要时滞环节。因此，实施起来方便，适应性强。

从图中可以看出，由主控制器G_c（s）与G_o（s）、G_m（s）、G_k（s）组成的主随动控制系统，用于使观测器输出值跟踪设定值。由副控制器G_k（s）与G_m（s）组成副随动控制系统，用于使观测器输出值与系统的输出保持同步。当设定值R变化时，由于观测器输出Y_M尚未变化，所以主控制器输出一个较强的控制信号，通过前馈作用，使观测器输出较快地跟踪，以减少控制器的偏差，起到超前的控制作用。同时，该控制信号对过程本身也起调节作用，使输出较快变化。由于副控制器的控制作用，使观测器输出Y_M适应系统输出Y的变化。当主、副控制器均为比例积分作用时，整个系统可以达到稳态无余差。

观测补偿器控制方案仅适用于随动控制系统，不适用于定值控制系统。