史密斯预估补偿控制方案优化

史密斯预估补偿控制的框图如图2-17所示，图中G_k（s）是史密斯引入的预估补偿器的传递函数。为使图2-17所示系统的闭环特征方程中不含有时滞τ，因此期望的闭环传递函数

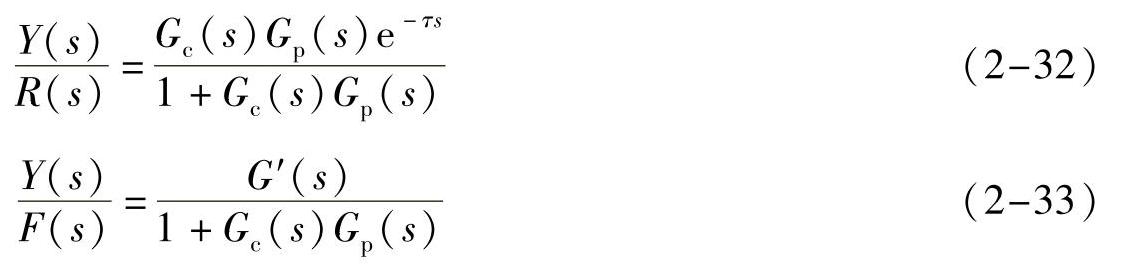
引入预估补偿器后，实际的闭环传递函数是

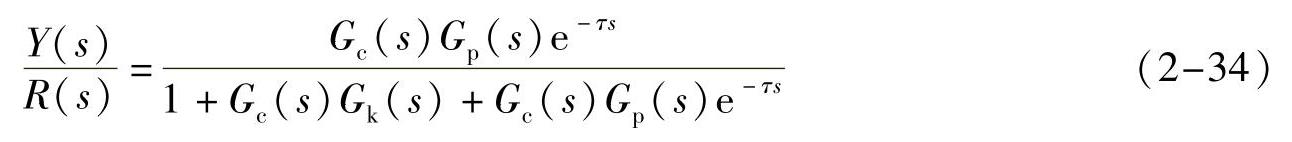
根据要求

1+G_c（s）G_k（s）+G_c（s）G_p（s）e^-τs=1+G_c（s）G_p（s）

所以 G_k（s）=G_p（s）（1-e^-rs） （2-35）

这样构成的预估补偿控制方案如图2-17所示，其闭环传递函数为

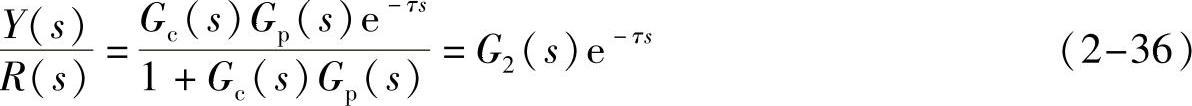(www.xing528.com)

其中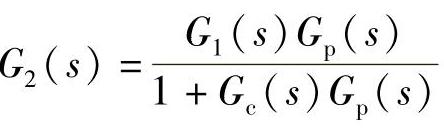，类似于没有时滞环节时的随动控制系统的闭环函数。同样，由图2-18可以得到定值控制系统的闭环传递函数

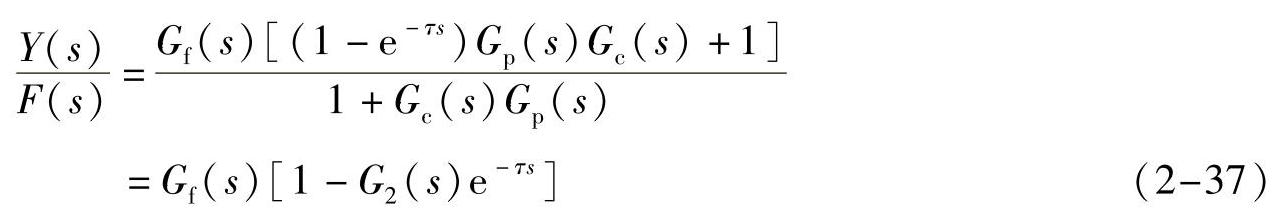
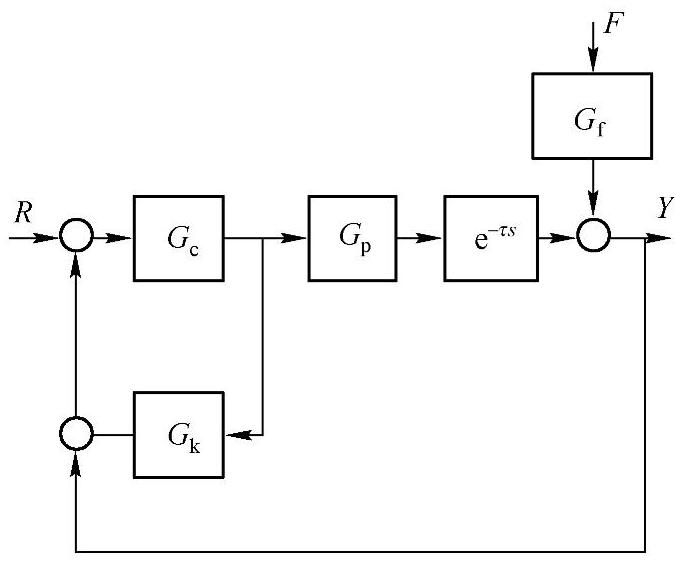
图2-17 史密斯预估补偿控制的框图

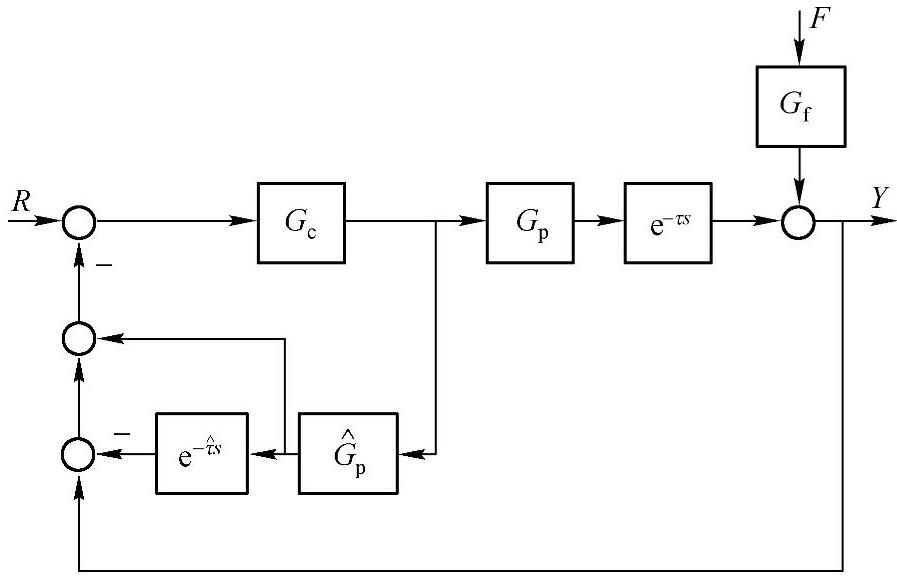
图2-18 定值控制系统的闭环传递函数

因此，经过预估补偿后，闭环特征方程中已消去了e^-τs项，也就是消除了时滞对控制品质不利的影响。对于随动控制系统，控制过程仅在时间上推迟时间τ。这样，系统的过渡过程形状与品质和无时滞的完全相同。对于定值控制系统，控制作用要比扰动滞后一个τ时间，所以控制效果不如随动控制系统那样明显。

随着电子计算机应用，特别是集散控制系统中实施更为方便，史密斯预估补偿器的应用近年日益普遍。这种补偿器不仅可用于单输入单输出系统，也可用于多输人多输出系统。史密斯预估补偿器对大时滞过程尽管能提供很好的控制质量，但遗憾的是，其控制质量对模型误差十分敏感，特别是时滞时间和增益误差。所以对非线性严重或时变增益的过程，这种线性史密斯预估器是不太适用的。