串接解耦控制优化策略

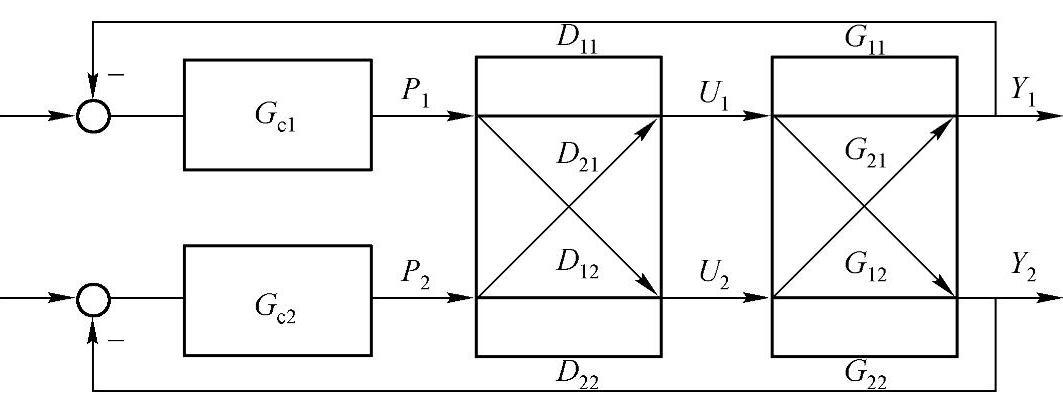
图2-13 双输入双输出串接解耦控制系统框图

图2-13所示为双输入双输出串接解耦控制系统框图。由图可得

Y（s）=G（s）U（s）

U（s）=D（s）P（s）

所以 Y（s）=G（s）D（s）P（s） （2-24）

由式（2-24）可知，只要能使G（s）D（s）相乘后成为对角阵，这样就解除了系统间耦合，两个控制回路不再关联。要求G（s）D（s）之积为对角阵，对其非零元素又有三类方法：

1.对角线矩阵法

此法要求G（s）D（s）=diag[G_ij（s）]，如

即通过解耦，使各个系统的特性完全像原来的单回路控制系统一样。

因此，解耦装置D（s）可以由式（2-25）求得

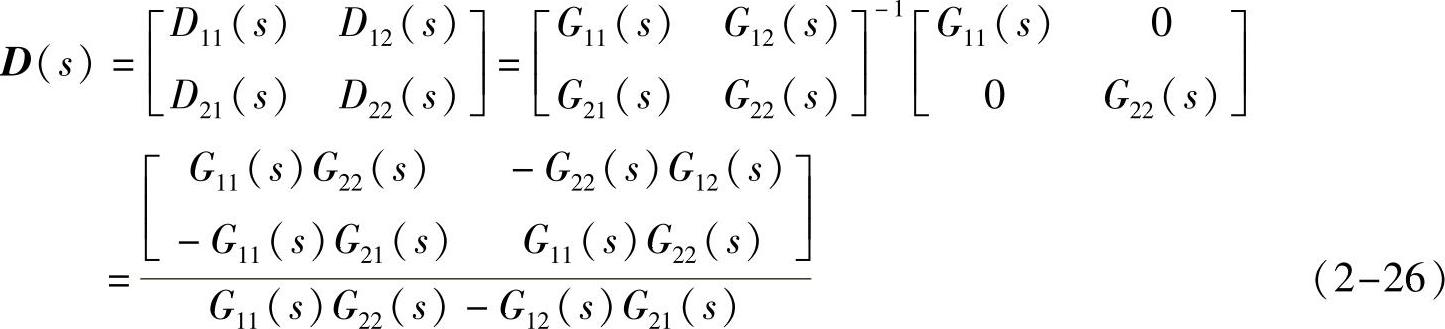
这样求得的解耦装置元素的传递函数可能相当复杂。

2.单位矩阵法

单位矩阵法为

G（s）D（s）=I=diag[1，1Λ1]

如 (www.xing528.com)

此时解耦装置D（s）为

这种方法解耦使各个系统的对象特性成为1∶1的比例环节，所以具有稳定性好、克服外扰能力强的优点。但是要实现它的解耦装置比其他方法求得的解耦装置更为困难。

3.前馈补偿法

前馈补偿法只规定对角线以外的元素为零，这样也完全解除了系统间的耦合。但各通道的传递函数并不是原来的G_ij（s）。此时可取某些G_ij（s）=1，这样做显然比较简单，所以也有人称之为简易解耦。

图2-14 前馈解耦控制系统框图

对于双输入双输出系统的前馈解耦控制系统框图如图2-14所示。在此取D₁₁（s）=D₂₁（s）=1，解耦补偿装置D₂₁（s）和D₁₂（s）可以根据前馈补偿原理求得

G₁₂（s）+D₂₁（s）G₂₂（s）=0

所以

又有 G₁₂（s）+D₁₂（s）G₁₁（s）=0

也可令D₂₁（s）=D₁₂（s）=1或D₂₁（s）=D₂₂（s）或D₁₂（s）=D₁₁（s）=1。

按同样原理可以求得解耦补偿装置的传递函数，在很多情况下，采用静态解耦已能获得相当好的效果。

一般来说，需要采用动态解耦时，D_ij（s）宜采用超前滞后环节即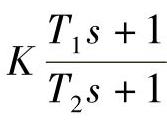的形式。