前馈补偿装置及控制技术

前馈补偿装置的复杂程度主要取决于控制通道和扰动通道的传递函数。在工业控制实际应用中，控制通道和扰动通道的传递函数可以用具有时滞一阶环节来近似，其传递函数分别为

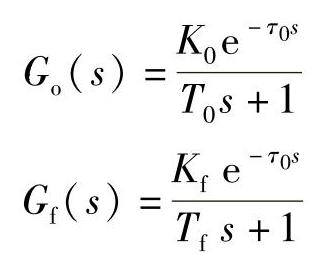
这样得到的前馈补偿装置的传递函数为

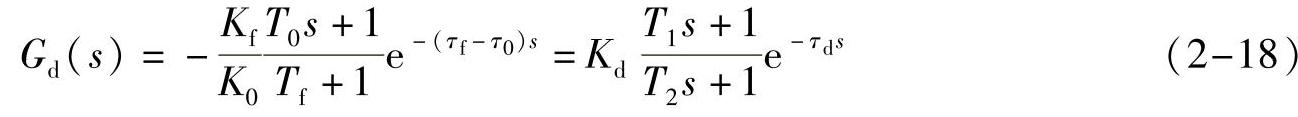
若τ₀=τ_f时，则可得

式中，K_d是静态增益；T₁和T₂分别是超前和滞后环节的时间常数。T₁＞T₂时，补偿环节具有超前特性，T₁＜T₂时，补偿环节具有滞后特性，T₁=T₂时，动态环节的分子分母项抵消，只进行静态补偿。

在用计算机控制时，前馈补偿装置与其他控制算法一样是用软件来实现的。实际上又可分为两类：一类采用组态形式，把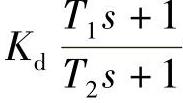作为一种组态；另一类是直接按u_d与f的关系计算。首先将前馈补偿装置的传递函数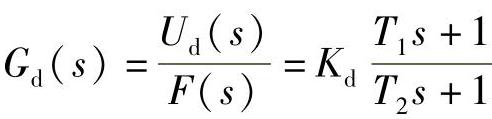转化成如图2-10所示等效框图。

由图2-10可知，先计算f→b

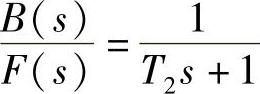
即

T₂sB（s）+B（s）=F（s）

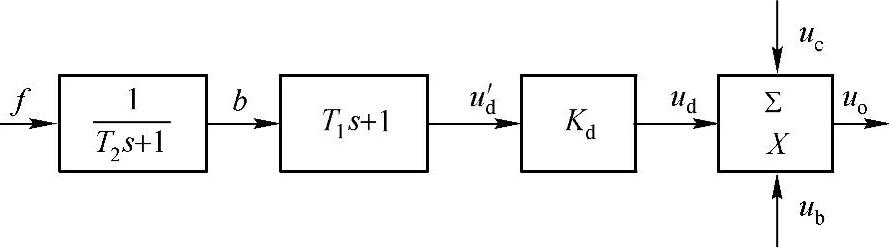
图2-10 等效框图

写成差分方程形式

所以

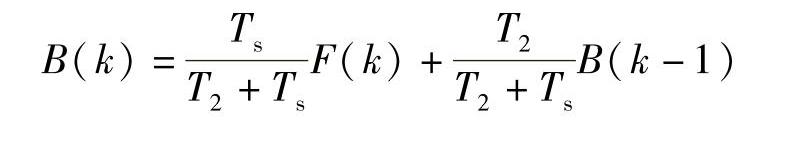
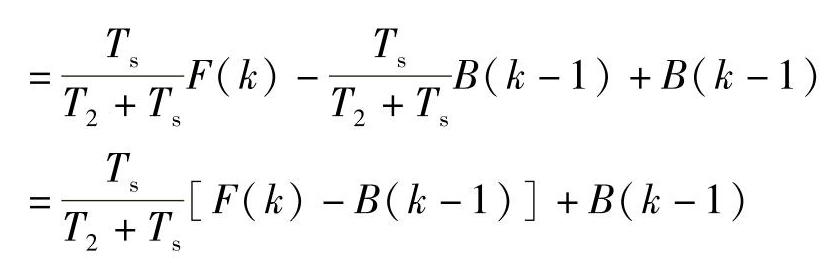
上式可写成

(https://www.xing528.com)

令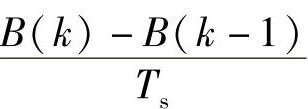=A或B（k）=AT_s+B（k-1）

即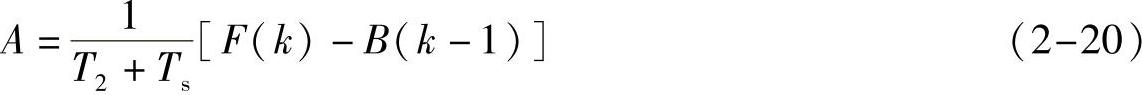

再计算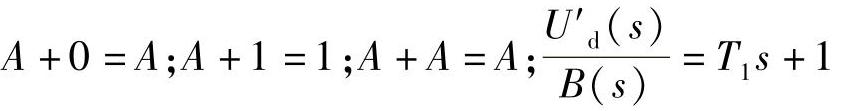

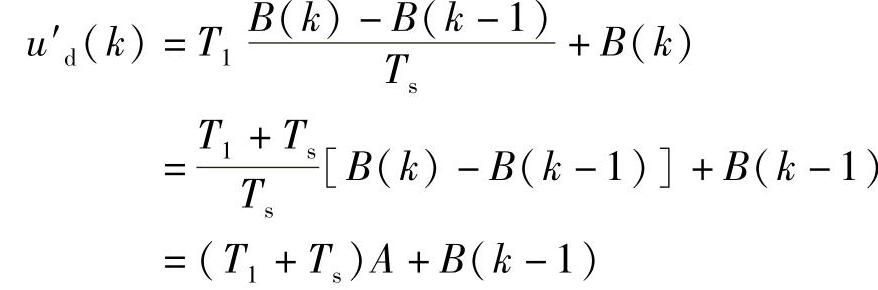
因此超前滞后环节的算法为

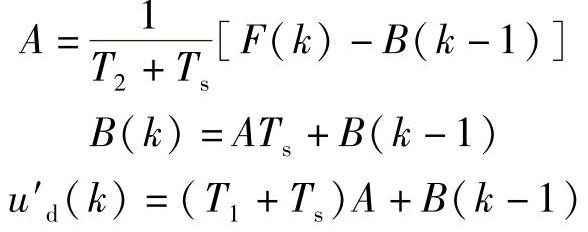
式中 A——中间变量；

F（k）——模块输入，前馈变量的现时值；

u′_d（k）——超前滞后环节的输出；

B（k）——F通过滞后环节的现时输出值；

B（k-1）——F通过滞后环节的上一次输出值；

T₁——超前时间；

T₂——滞后时间；

T_s——采样周期。

这类补偿环节的输出有两类：

1）比值算法（用于相乘方案）：u=[K_du′_d/u_b]u_c

2）位置算法（用于相加方案）：u=[K_du′_d-u_b]+u_c

式中 u_b——偏置；

u_c——反馈输入。