改进理想PID控制算法的优化方案

1.积分算法的改进

引入积分作用的目的是消除误差，离散PID控制算法中的积分控制作用有三点值得改进。

（1）圆整误差问题

在位置算法中积分作用的输出为

在增量算法中积分作用的输出为

由于工业计算机往往采用定点计算，存在字长精度限制的问题，当运算结果超过机器字长精度表示的范围时，计算机就将其作为机器零而把此数丢掉。下面举例说明定点计算机对积分项运算结果的影响。

例如，当控制某炉出口温度时，设定值R为1600℃，测量值y（k）为1605℃。机器字长为十进制4位，定点设定在最高位，则偏差用定点可表示为

e（k）=R-y（k）=0.1600-0.1605=-0.0005

若取K_I=0.1，则Δu（k）=0

也就是说，机器计算的结果没有起到积分作用，使偏差5℃始终存在，误差无法消除，只有当偏差≥10℃时，才有积分项的输出，所以误差将达10℃。增强积分的作用，可以减小误差。但积分作用的增强往往会使系统振荡加剧，降低稳定性裕度，有时又不允许。为此需要改进，常用的办法是在机器内增加∑e（i）累加单元。当Δu_I（k）出现机器零时，开始把e（k）保留在累加单元内，到下一次采样输入时，把e（k+1）与它相加起来，看Δu_I（k+1）是否大于机器零，如仍不行，则一直累加到Δu_I（k+i）不为零为止，此时将Δu_I（k+i）输出，并把累加单元清零。这样，通过程序编制的改进，解决了由于定点运算的字长限制而丢掉积分作用的问题。

（2）积分分离

采用连续PI控制算法，比例控制作用u_p和偏差e是同步的，而积分作用u_I却落后1/4周期。因此积分作用虽然对消除误差有益，但相位滞后是加剧振荡的根源。

在离散PID控制算法中，可以通过下列途径来改变这一情况。

一种办法是只在u_I和u_p同方向时，才把积分作用引入；而在u_I与u_p反方向时，把u_I切除，这在计算机上是很容易办到的。

另一种办法是只在|e|小于某一界限时，即被控变量相当接近设定值时，才把u_I引入，而在其余情况下，把u_I切除。图2-2为具有积分分离控制算法的控制效果比较。

图2-2 具有积分分离的控制过程

由图可见，采用积分分离算法时，在达到同样的衰减比下，显著地降低了被控变量的超调量，大大缩短了过渡过程的时间，提高了系统的品质。

（3）数值积分的改进

虽然PID控制算法中积分项对跳码和噪声的敏感性比微分项要小，但是如果用梯形求积公式

代替矩形求积分∑e（k）进行数字积分，可提高积分计算的精度且少受噪声的影响。当然，它要付出一定的代价，即要求增加计算时间和内存容量。

2.微分算法的改进

（1）微分先行

微分先行是只对被控变量求导，而不对设定值求导。这样，在改变设定值时，输出不会突变，而被控变量的变化，通常总是比较缓和的。此时的控制算法为(www.xing528.com)

Δu_d（k）==K_D[y（k）-2y（k-1）+y（k-2）] （2-10）

微分先行的控制算法明显改善了随动系统的动态特性，而静态特性不会产生影响，所以这种控制算法在模拟式控制器中也被采用。

（2）不完全微分

不完全微分是用实际的PD来代替理想的PD环节。这样，在偏差有较快变化以后，微分作用一下子不会太剧烈，可保持一段时间，在模拟式控制器中就是这样做的。在离散PID控制算法中，P、I、D三个作用是独立的，因此，可以整体地串接一个环节，也就是说串接一个低通滤波器，把它接在输入端比接在输出端更为合适，如图2-3所示。

图2-3 微分先行

在同样阶跃输入下，采用同样PID参数，完全微分与不完全微分PID的输出如图2-4所示。

图2-4 完全微分与不完全微分PID的输出

a）完全微分 b）不完全微分

（3）四点中值差分法

为了减少噪声的影响，输入滤波是必要的，上述不完全微分就是一种输入滤波。除此之外，应用很成功的一个方法就是采用四点中值差分。把e（k）、e（k-1）、e（k-2）、e（k-3）四者的平均值作为偏差进行差分运算

即取这四点e～t平面上与中点作连线，求取各自的斜率，把斜率的平均值作为e（k）的导数，即

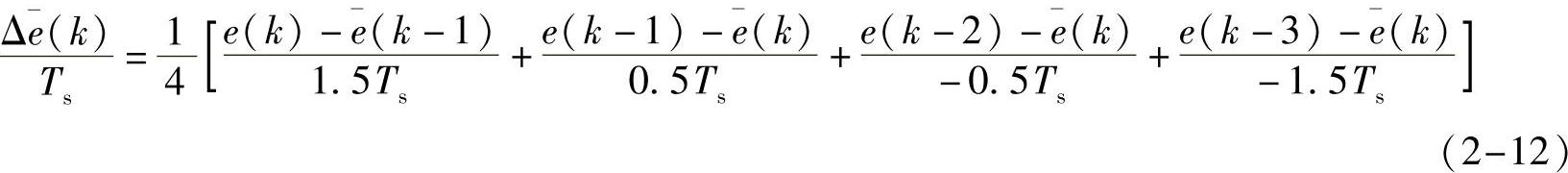
整理上式可得

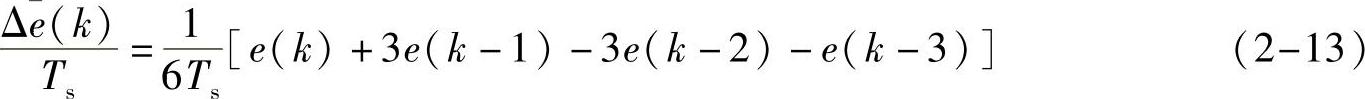
如采用位置算法，就取值代替如采用增量法，取

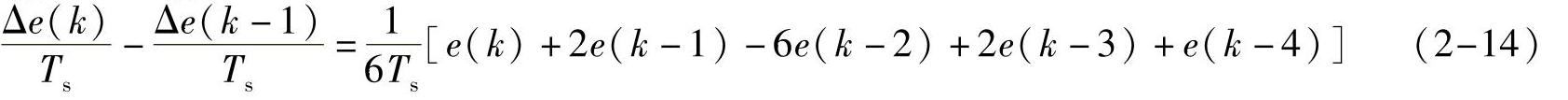
3.带有不灵敏区的PID控制算法

对于某些要求控制作用尽量少变的场合，可以采用带有不灵敏区的PID控制算法，即

式中 B——不灵敏区；

u（k）——控制器第k时刻的输出；u（k-1）——控制器第（k-1）时刻的输出。

这种算法实质上属于非线性控制。例如两个精馏塔之间的平稳操作，前塔的出料作为后一塔的进料时，为了使操作平稳，要求前塔塔底液位和后塔进料流量波动尽量小。通常可以采用均匀控制，但也可采用具有不灵敏区的PI控制算法作为液位控制。只要液位偏差不超过规定的B，出料流量就不改变；只有当液位偏差大于B时，才控制出料量，从而克服了不必要的流量波动。