实现理想PID控制的优化算法

设定值r与测量值y相比较，得出偏差e=r-y，并依据偏差情况，给出控制作用u。在时间连续类型，理想PID常用的表示形式为

或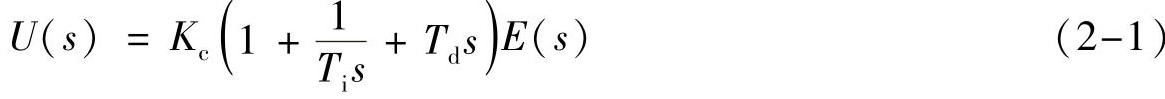

式中 K_c——控制器比例增益；

T_i——积分时间；

T_d——微分时间。

在上述控制算法中，只包含第一项时，称为比例（P）作用；只包含第二项时，称为积分（I）作用；只包含第三项时，称为微分（D）作用（但不采用，因为它不能起到使被控变量接近设定值的效果）；只包含第一、二项的是比例积分（PI）作用；只包含第一、三项的是比例微分（PD）作用；同时包含这三项的是比例积分微分（PID）作用。

在离散控制系统中，要把PID控制算式进行离散化处理，以便实现计算机控制。

离散PID控制算法可分为三类：位置算法、增量算法、速度算法。

1.位置算法

理想PID控制算法很容易从式（2-1）得到

或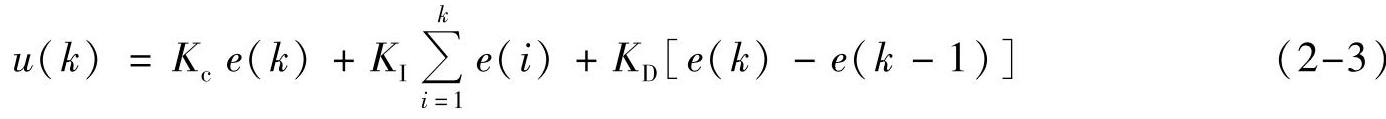

式中 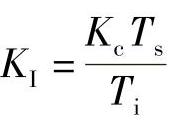——积分系数；

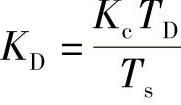——微分系数；(https://www.xing528.com)

T_s——采样周期。

式（2-2）或式（2-3）是理想PID位置算法，它的输出u（k）与控制阀（或执行器）的开度（位置）是一一对应的。这种算法需要计算机重复计算每一时刻区间阀位的绝对值。

2.增量算法

PID控制增量算法为相邻两次采样时刻所计算的位置值之差，即

设 Δe（k）=e（k）-e（k-1）

则 Δu（k）=K_cΔe（k）+K_Ie（k）+K_D[Δe（k）-Δe（k-1）] （2-5）

式（2-4）或式（2-5）就是理想PID控制增量，其输出Δu（k）表示阀位的增量，控制阀每次只按增量大小动作。

3.速度算法

速度算法是增量算式除以采样周期T_s，即

三种算法的选择，一方面要考虑执行器的形式，另一方面要分析应用时的方便性。从执行器形式来看，位置算法的输出除非用数字式控制阀可直接连接外，一般须经过D/A转换为模拟量，并通过保持电路，把输出信号保持到下一个采样周期的输出信号到来时为止。增量算法的输出可通过步进电动机等累积机构化为模拟量。而速度算法的输出须采用积分式执行机构。

从应用方面来看，采用增量算法和速度算法，手/自动切换都比较方便，是因为它们可以从手动时的u（k）出发，直接求取在投入自动运行时应该采取的增量Δu（k）和变化速度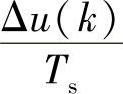。另外，这两类控制算法还不会产生积分饱和现象，是因为它们求出的是增量和速度，即使偏差长期存在，Δu（k）一次次地输出，使执行器达到极限位置，但只要e（k）换向，Δ_u（k）也即换向，输出立即脱离饱和状态。当然，加上一些必要措施，手/自动切换和积分饱和问题在位置算法中也可以解决。