子模型接触分析的流程优化

首先进行全局模型的计算。为了在保证计算精度的前提下尽量减小计算规模，需要对机体与隔板的计算模型进行适当的简化，主要有以下几个方面：

（1）通过前面章节的分析可知，机体上某一隔板上的应力分布主要由与其相邻的作用力决定，远离该隔板的其他载荷对其应力分布影响很小。因此，本节选取机体的1/4模型进行分析，计算用几何模型如图8.2所示。

（2）通过对所研究机型结构和安装方式的分析可知，机体中间位置的隔板远离机体紧固支撑位置，刚度较低，应力水平较高，是整个结构的薄弱环节，通过对多体动力学计算结果的分析发现，第2隔板承受的载荷较大，因此选取第2隔板进行有限元分析。

（3）由于本节主要研究机体隔板与主轴承座螺栓紧固连接位置的微动疲劳问题，因此对隔板上的细小结构进行了适当简化，计算主要针对机体隔板与主轴承盖的接触问题进行求解，主要分析不同工况下该接触面的接触状态和应力-应变场分布情况。

图8.2　有限元接触计算使用的机体隔板与主轴承盖的几何模型

接触问题是高度非线性问题，对计算模型和求解设置要求很高。根据有限元接触算法的要求，接触分析通常采用一次单元。本章采用8节点六面体单元对几何模型进行有限元划分，因为是全局模型计算，因此对接触区局部网格未进行加密，整体模型应用尺寸约为3 mm×3 mm×3 mm的单元划分。整个有限元模型共划分单元865 003个，如图8.3所示。

图8.3　机体隔板与主轴承座装配体的有限元计算模型

根据该发动机的装配要求，机体隔板与主轴承盖之间的4根预紧螺栓的预紧力均为Fbolt=147 000 N。由多体动力学计算结果可知，活塞侧击力与气体力和主轴承载荷相比较小，对机体隔板与主轴承盖接触行为影响很小，因此在计算中不考虑活塞侧击力的作用。在各气缸上端面气缸中心线上建立参考点，将其与相应气缸上端面上的节点绑定，用于施加气体力，如图8.4所示。疲劳分析主要关注结构应力或应变的变化情况，因此选取1、2、3、4各缸爆发的时刻进行计算。在各缸绑定连接参考点上分别施气体作用力Fgas1、Fgas2、Fgas3、Fgas4，注意到计算模型分别取各气缸的1/2，因此加载气体作用力时施加各缸气体中作用力的1/2；在主轴承盖和机体隔板组成的圆环面上施加轴承力Fbearing，主轴承载荷为分布载荷，按余弦形式分布在120°范围内，其分布形式如图8.5所示，其表达式为

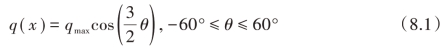
式中，qmax为轴承力分布载荷的峰值。

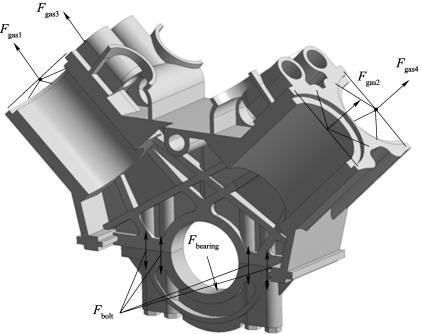
图8.4　有限元计算的载荷边界条件

将机体隔板与主轴承盖的接触面定义为接触，定义接触行为遵循库仑摩擦定律，通过查阅相关资料，定义接触面的摩擦系数μ=0.54。(www.xing528.com)

对于本章所选取的1/4机体计算模型，根据结构的对称性，分别约束剖切截面上节点的法向自由度，通过施加该对称约束来消除模型的刚体位移。

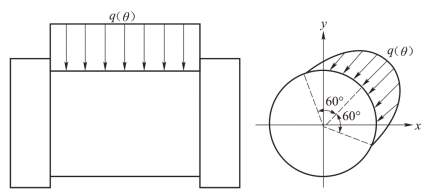
图8.5　轴承载荷的分布形式

定义两个分析步，第一步施加螺栓预紧力，在机体隔板与主轴承盖间建立接触；第二步施加气体作用力和主轴承载荷。

得到全局模型的计算结果后，将全局模型的计算结果映射到子模型上，同样定义子模型中对应于主轴承盖和机体隔板的接触面为接触，采用与全局模型相同的单元类型划分网格，网格尺寸为0.1 mm×0.1 mm×0.1 mm。

子模型的整个分析流程如图8.6所示，主要分为以下几步：

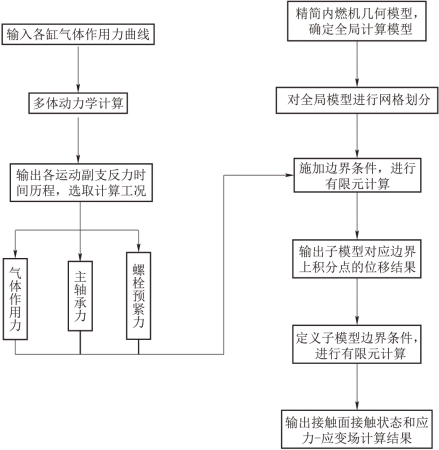
图8.6　机体隔板与主轴承座子模型有限元接触分析流程

（1）通过多体动力学分析得到整机在一个典型工作循环中的载荷时间历程。

（2）选取全局模型，对几何模型进行适当简化并划分网格。

（3）确定载荷边界条件和位移边界条件进行全局模型的计算。

（4）将全局模型的计算结果映射到子模型的相应边界上进行子模型计算。

结构模型的子模型计算流程与机体隔板及主轴承座的计算流程相似，这里不再赘述。需要说明的一点是，试验试件的两端用螺栓紧固在试件夹具上，由于夹具的刚度很大，可近似为固定约束。仿真计算时约束试验试件两侧面上节点的所有自由度以消除模型的刚体位移。有限元计算所采用的几何模型和有限元模型如图8.7所示。

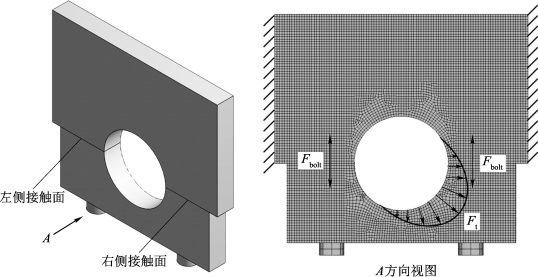
图8.7　结构模型的几何模型和有限元模型