对螺栓预紧力的精确控制是该试验的另一个关键问题。一般来说,控制螺栓预紧力的方法主要有以下3种:
1.通过拧紧力矩控制预紧力
螺栓未发生塑性变形时,拧紧力矩与预紧力之间存在线性关系,控制了拧紧力矩的大小,就可计算出所施加的预紧力。工程应用的拧紧力矩和预紧力之间的计算公式为
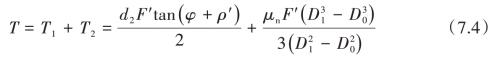
式中,T1为螺旋副间的螺纹力矩;T2为螺母支撑面上的摩擦力矩;d2为螺纹中径;φ为螺旋升角;ρ'为摩擦角;μn为摩擦系数;F'为预紧力;D1为螺母支撑面外径;D0为螺母支撑面内径。
目前,工程上广泛应用控制拧紧力矩的方法来控制螺栓预紧力。但是由于摩擦系数和几何参数的偏差影响,在一定的拧紧力矩下,预紧力值的离散性比较大。通过拧紧力矩控制预紧力的方法精度不高,预紧力的偏差可达±40%。
2.通过螺母转角控制预紧力
因为螺栓的螺距是一定的,因此在一定范围内通过测量拧紧螺母的转角,可以计算出螺栓的伸长量,从而可换算得到螺栓的预紧力大小。在实际操作中,通过标记零线的方法,螺母转角测量精度可控制在10°~15°。
由于接触变形,螺母与支撑面完全接触的开始位置较难确定,加之被连接件的刚度(变形)计算较为复杂,螺栓出现扭转变形、紧固件尺寸误差等因素,通过该方法控制预紧力的误差大概为±15%。
3.通过螺栓伸长控制预紧力
因为螺栓的伸长只与螺栓的应力有关,可以排除摩擦系数、接触变形和被连接件变形等可变因素的影响。因此通过测量螺栓的伸长量来控制预紧力可获得最高的控制精度。通常,在长度测量精度为1μm时,长度为20~25 mm的螺栓,其预紧力误差可控制在±5%。
该方法虽然控制精度较高,但是应用受到限制,对于拧紧在盲孔中的螺栓可操作性较差。
综合以上螺栓预紧力控制方法和本书研究的结构模型的特点,兼顾控制精度和可操作性,本书采取一种间接测量的方法来控制螺栓预紧力。通过上面介绍的预紧力控制方法可发现,要提高螺栓预紧力的控制精度,应尽量避免测量与摩擦力和接触变形等不确定因素相关的参数。直接测量螺栓连接各部分的变形量是控制预紧力行之有效的方法。考虑到本书中应用的结构模型尺寸和空间位置的限制,测量螺栓的伸长量难度较大,本书采用测量被连接件(压头)的被压缩量的方法来控制螺栓预紧力。在弹性范围内构件的变形与应变是线性相关的,在实际应用中应变易于测量,因此通过测量压头的应变来控制螺栓预紧力是可行的。
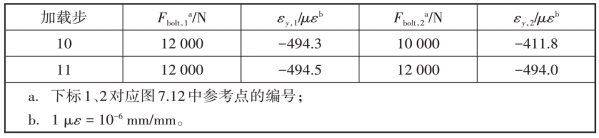
应用这一方法的关键是得到应变与螺栓预紧力的关系。本章首先建立结构模型的有限元模型,计算不同螺栓预紧力条件下压头上同一点的应变值,从而得到应变与螺栓预紧力的关系。计算采用的有限元模型如图7.11所示。本计算分11步进行加载,为在压头和试件间建立接触关系,第一步施加一很小的螺栓预紧力,然后依次施加4 000~12 000 N的螺栓预紧力并读取夹头表面距上端面11 mm,距侧端面18 mm处的两个参考点(见图7.12)的y方向(见图7.11)应变。另外,在分步施加螺栓预紧力时,一侧螺栓预紧力固定,只增加另一侧的预紧力。其目的在于考察一侧螺栓预紧力对另一侧螺栓受力的影响。加载步骤和应变计算结果如表7.3所示。
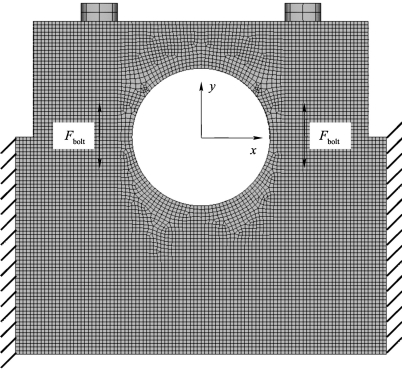
图7.11 螺栓预紧力有限元计算模型
从表7.3可以看出,一侧螺栓加载时对另一侧螺栓的预紧力几乎没有影响,不存在耦合关系。因此可以通过一侧的螺栓预紧力和参考点应变数据得到两者的关系。对预紧力和应变数据进行线性回归发现,应变与预紧力存在确定的线性关系:(https://www.xing528.com)
Fbolt=-24.3εy (7.5)
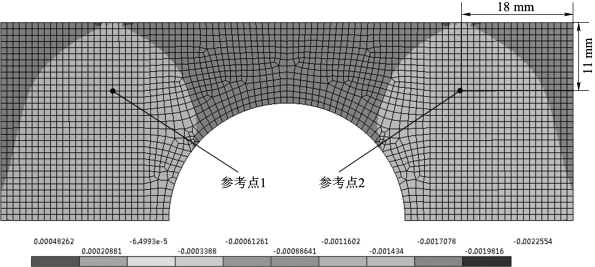
图7.12 应变参考点位置和压头应变分布
表7.3 螺栓预紧力有限元计算的加载步设置和参考点处的应变
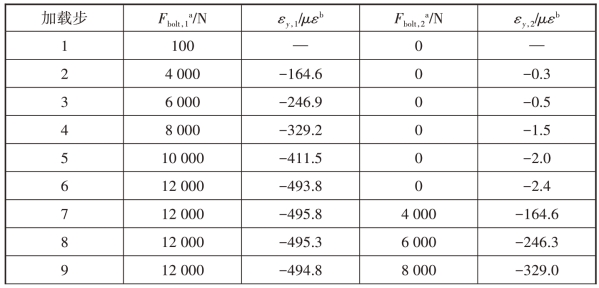
续表
对仿真结果进行了螺栓拧紧试验。在压头上有限元计算的参考点位置粘贴应变片,将其与动态应变仪桥盒连接组成1/4电桥。电桥电路如图7.13所示。电桥信号通过动静态应变仪放大后以电压的形式显示,通过电压与应变的换算可得到应变片粘贴位置的应变信息。记录螺栓拧紧时参考点位置的实际应变,从而对仿真计算进行验证。试验实物如图7.14和图7.15所示。试验结果见表7.4。
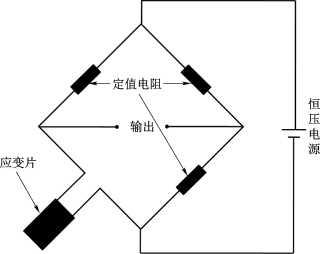
图7.13 恒压1/4电桥电路

图7.14 螺栓拧紧试验实物
由表7.4的试验数据可见,有限元仿真结果与实际情况相符合,可以应用式(7.5)对螺栓预紧力进行控制。
表7.4 螺栓拧紧试验数据


图7.15 动态应变仪与动态应变仪桥盒
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




