有限元分析结果优化

使用6.5节建立的有限元模型，分别计算了k=1.0，1.5，2.0时最大横向载荷工况的应力分布。横向荷载方向的应力σy分布如图6.6所示，从应力云图可以看出，在远离螺栓孔的部分，试件所受的正应力是均匀分布的。应力集中出现在孔边缘附近和接触边缘附近。随着k的增加，孔边缘应力集中效应的影响逐渐减小，而接触边缘区域周围的应力梯度逐渐增加。为了更好地理解，定义应力集中系数kc为

式中，σmax为孔边缘处的最大应力；σn为试件远端的均布应力。

不同载荷条件下应力集中系数如表6.1所示。

图6.6　横向应力σy的分布

（a）k=1.0；（b）k=1.5；（c）k=2.0

表6.1　不同载荷条件下的应力集中系数

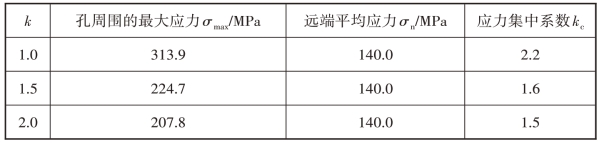
作为一个接触问题，接触相关因素对于螺栓连接的疲劳性能有非常重要的影响。图6.7～图6.9分别给出了接触面上的接触应力分布、滑移量和接触状态。图6.7指出，最大接触应力出现在拉伸方向的螺栓孔边缘。随着k的增加，最大接触应力相应增加。尽管连接件被螺栓预紧力夹紧，但是各部分变形的不一致会导致接触区域的边缘部分发生滑动，这就是微动的来源。如图6.8所示，k的增加对滑移具有抑制作用。值得注意的是，对于k=1.0的情况，几乎整个接触区域都为滑移区，这时螺栓连接不能通过摩擦很好地传递载荷，整体处于滑动状态。图6.9显示随着k的增加，如图例所示的closed（slipping）区域，即滑移区逐渐减小，而图例所示的closed（sticking）区域，即黏着区逐渐增大。虽然理论上被连接件的重叠位置都是接触的，但是根据圣维南原理，螺栓预紧力只能影响其周围的有限区域。因此，图例所示的open区域，即不接触区域的大小，在参数k取不同值时没有明显的变化。在k=1.0的条件下，接触界面处于全局滑动状态，如图6.8（a）所示。(www.xing528.com)

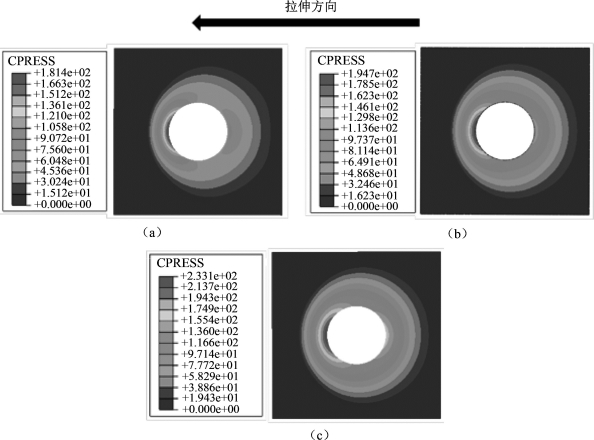
图6.7　接触应力分布

（a）k=1.0；（b）k=1.5；（c）k=2.0

图6.8　接触区滑移量分布

（a）k=1.0；（b）k=1.5；（c）k=2.0

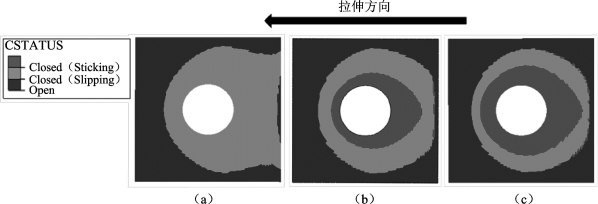
图6.9　接触区接触状态

（a）k=1.0；（b）k=1.5；（c）k=2.0

从有限元分析可以推断，施加在螺栓上的预紧力会导致被连接件的压缩，并避免（或缓解）螺栓紧靠孔边缘的状态。因此，大部分横向载荷可以通过被连接件间的摩擦力来传递。通过这种方式，横向载荷被分散到螺栓孔周围的较大区域上，进而导致应力集中系数逐渐减小。