微动疲劳属于多轴疲劳问题,而分析多轴疲劳最有效的方法为临界面法。应用临界面法预测疲劳损伤的首要工作是确定临界面的方向。对于微动疲劳还需确定临界面的位置。接触面上的应力场分布如图4.7所示。在法向接触压力、远端交变载荷以及切向牵引力的共同作用下,接触面上一点处的应力状态为典型的多轴应力状态。一点处任意方向上的应力-应变状态可以由以下变换方程求出:
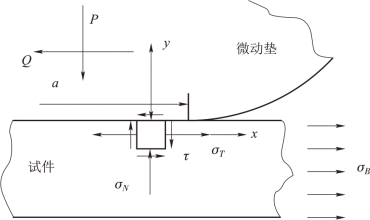
图4.7 接触区表面一点处的应力状态
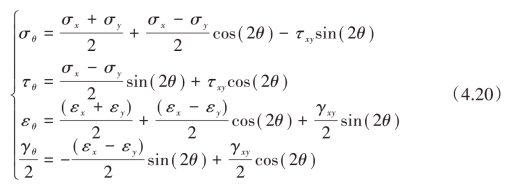
要确定微动疲劳裂纹萌生位置和初始扩展方向,即确定临界面的位置以及其与接触面的角度。本书应用MATLAB编写了确定临界面方向和位置的程序,程序代码见附录2,计算流程如图4.8所示。由于接触状态在试件最大受拉工况和最大受压工况间变化,其接触应力近似为正弦变化,相应峰值也出现在以上两个位置。因此计算应力(或应变)范围时只需上述两个时刻的应力(或应变)分布即可。首先将有限元计算结果输入程序,根据式(4.20)按照0.1°的步长,计算与接触面呈θi(-90°≤θi≤90°)角度的平面上的正应力(正应变)和切应力(切应变),然后判断临界面的位置和角度。本书所选的疲劳模型均以最大切应力(或应变)范围平面为临界面,因此本程序通过计算各位置和角度上的切应力(或应变)范围,以切应力(或应变)范围最大的平面的位置、角度为临界面。最后输出计算结果,得到裂纹萌生位置和初始扩展方向的分析结果。式(4.20)计算得到的角度值为临界面的法向与接触面的夹角,并规定逆时针方向为正,相应的初始裂纹扩展方向为临界面方向,规定以接触面法向为参考,顺时针方向为正。因此,计算得到的角度值与裂纹初始扩展角度互余,它们之间的关系如图4.9所示。计算结果参见附录3。从计算结果可见,所有的裂纹萌生位置均在远端交变载荷作用端靠近接触区边缘的位置(x/a=0.881~0.991),裂纹的初始扩展方向在48.3°~50°(或-41.7°~-40°),与试验现象相符。(https://www.xing528.com)
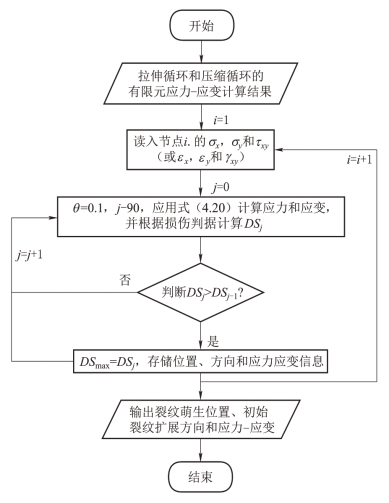
图4.8 微动疲劳裂纹萌生位置和初始扩展方向预测方法流程
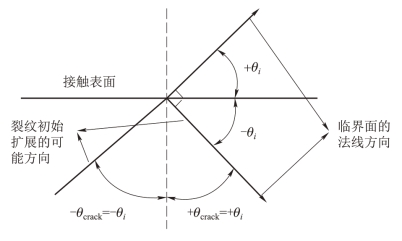
图4.9 临界面法向与裂纹初始扩展方向的关系
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




