建立微动损伤相关系数

总结4.2.1节讨论和分析得出的结论，基于以下4个概念建立适用于微动疲劳的微动损伤相关系数：

（1）滑移幅值δ是影响材料和结构的微动疲劳行为的最主要的参数之一。滑移使疲劳寿命降低，尤其是在部分滑移状态下。

（2）在微动过程中，切向牵引力幅值Q与滑移幅值δ是正相关的，切向牵引力幅值Q可以用于表征滑移幅值δ的大小。进一步可以应用Q对微动作用的强度进行定量描述。本书采用对微动损伤进行定量描述。

（3）在相同的应力（或应变）水平下，由于微动作用的存在，材料和结构的微动疲劳寿命比普通疲劳低。由于微动效应的存在，疲劳损伤参量的作用被放大了。

（4）微动疲劳损伤模型与普通疲劳损伤模型有着相同的形式，可以通过对普通疲劳损伤模型的改造来预测微动疲劳损伤。

基于以上4个概念，本书提出的微动相关系数FRD可表述为

式中，α，β为常数，α≥1，β＞0；μ为滑动摩擦系数。因此，FRD是一个大于1的参数。根据库仑摩擦定律，只有当切向牵引力与接触面滑动摩擦力的比值Q/μP=1时，接触区处于全局滑移状态，此时无黏着区存在；当0＜Q/μP＜1时，表明接触区处在局部滑移状态，此时接触区中心部位为黏着状态。当接触区状态处于部分滑移时，材料或构件的失效形式体现为微动疲劳。另外，很多初始接触状态为全局滑移的情况，在经过若干次循环后，由于摩擦系数的增加也会转变为部分滑移状态。考虑到微动疲劳几乎都出现在局部滑移状态下，因此本书提出的FRD参数适用于接触状态为局部滑移的情况，这也符合库仑摩擦定律的规定，具有明确的意义。因为切向牵引力与滑动幅值之间存在正相关性，因此，Q/μP不仅能描述接触区的接触状态，还可以描述微动作用的大小。当Q/μP的值趋于零时，意味着滑移幅值和切向牵引力幅值都很小，此时微动对材料的损伤作用很微弱；相反的，随着Q/μP的增加，表明滑移幅值和切向牵引力幅值都在增加，此时微动对材料的损伤作用逐渐增强。

由于能更好地反映微动损伤的变化规律，因此本书采用其构建FRD参数。与Q/μP有着相同的单调性。值得注意的是，随着Q/μP的增加，的梯度下降。这一特性可以反映出随着滑移幅值和磨损率的增加，微动作用的剧烈程度会有所下降这一趋势。如4.2.1节所讨论的，随着微动状态逐渐接近全局滑移，磨损率随之快速增加，导致微裂纹更容易被磨掉而不是继续扩展。因此，微动对疲劳损伤的作用被弱化了，虽然仍保持增长的趋势，但强度有所下降。(www.xing528.com)

如图4.5所示，微动疲劳的S-N曲线与普通疲劳的S-N曲线存在一定的相似性，两者所反映的损伤参量与疲劳寿命之间的关系是相同的。将微动疲劳的S-N曲线向上移动就可以与普通疲劳的S-N曲线基本吻合。也就是说，将微动疲劳的损伤参量DPFF乘以一个大于1的系数即可得到同等载荷条件下的普通疲劳损伤参量DPPF，即有

FRD·DPFF=DPPF　（4.2）

那么，微动疲劳的损伤模型可以通过改造普通疲劳的损伤模型得到

FRD·DPFF=f(Nf)　（4.3）

将式（4.1）代入式（4.3），整理得

式中，和DPPF/DPFF为变量，可以由相关的微动疲劳试验数据和疲劳损伤模型求出；α，β为待定系数，与材料和损伤参量相关。通过对试验数据的分析计算可以得到α和β的值。

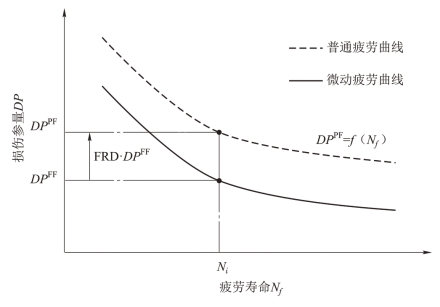
图4.5　建立微动疲劳损伤模型的原理