微动疲劳接触区有限元应力场分析

接触区应力场分析是进行微动疲劳损伤研究的重要基础。通过接触分析得到的接触区的应力应变分布是裂纹萌生位置、裂纹初始扩展方向和微动疲劳损伤的主要控制参数。有限元法作为成熟的数值分析方法，可以解决诸如接触这种高度非线性的问题。

对于如图2.1所示的接触问题，在圆柱面的轴线方向，力场的分布是一致的，因此可以将该问题简化为二维平面问题以减小计算量。同时该结构又存在着对称性，因此可以选取1/2模型进行计算。本书应用商用有限元软件ABAQUS对该问题进行建模和计算。有限元模型如图2.19所示。材料为2024-T351铝合金，材料参数如表2.1所示。模型分为三个主要部分：微动垫、试件和横向弹簧。为缩小计算规模，微动垫只建立接触区附近的部分，试件沿轴线取其一半建模，在其左侧边界和下边界上施加对称约束，在其右边界施加远端交变载荷σB。为了约束微动垫的刚体位移，在微动垫左侧建立横向弹簧区域。横向弹簧作为刚性支撑约束微动垫x，y方向上的刚体位移。赋予横向弹簧区域的单元极小的弹性模量（1 MPa），因此只有极小的载荷传递到该区域，不会对接触计算造成影响。切向牵引力Q按均布载荷施加在微动垫的左侧边界上。同样的，法向载荷P也按均布载荷施加在微动垫的上边界。为保证微动垫在受力时不发生偏转，耦合微动垫上边界节点的自由度，使其在y方向具有相同的位移。

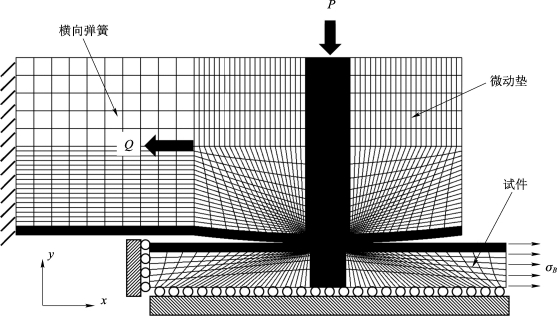
图2.19　接触分析的有限元模型

计算时模型按三步加载，第一步施加一个较小的法向载荷在微动垫和试件间建立接触；第二步施加计算所需的法向载荷；第三步施加远端交变载荷σB和对应的切向牵引力Q。

表2.1　铝合金2024-T351的基本力学性能参数

(https://www.xing528.com)

接触分析为高度非线性问题，接触区有限元网格的质量和单元尺寸直接影响到计算的收敛性和精度。因此对接触区的网格进行了加密，使用尺寸为10μm×10μm的正方形网格可以满足计算要求。将微动垫和试件的对应区域定义为接触，接触行为遵循库仑摩擦定律，参考相关文献，取滑动摩擦系数μ=0.65。该模型的计算结果与解析解的对比证明，该模型的精度很高，接触压力的计算结果误差小于2%。

试件上接触区域的典型应力分布如图2.20和图2.21所示。图中实线和虚线分别表示试件受最大拉伸载荷作用时和受最大压缩载荷作用时的应力场分布。可见，对于接触面上的切应力，拉伸循环和压缩循环的应力分布存在明显的对称性。在黏着区和部分滑移区的交界位置存在应力突变。法向正应力的分布没有明显的对称性，在接触区的边缘存在明显的应力突变；应力发生突变的位置是黏着区与部分滑移区的分界线，应用切应力分布判断更为明显。

图2.20　接触区切应力的典型分布（Q/μP=0.5，σB/μp0=0.5）

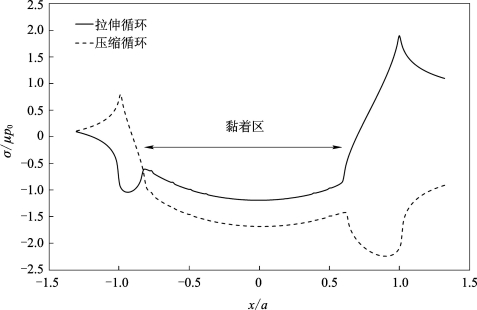
图2.21　接触区切向正应力的典型分布（Q/μP=0.5，σB/μp0=0.5）