经过Hertz、Mindlin、Nowell以及Hills等的研究工作，非协调接触问题已经得到很好的解决。然而，对于面-面接触即所谓的协调接触问题，求解难度较大。首先，两接触表面之间无初始间隙，这样就不能简单地通过二次多项式来描述；另外，协调接触表面常常不符合Hertz理论的应用条件，在载荷的作用下，接触区的尺寸迅速扩大，可能变得与接触体本身的有效尺寸相当，因此接触体不能再等效为弹性半空间。
对于实际工程中零部件间的平面接触问题，由于接触区边缘大多存在加工圆角，因此可将问题描述为如图2.6所示的带圆角的平面接触问题。圆角半径为R的平底物体在法向载荷P和切向载荷Q的作用下与弹性半空间发生接触并发生变形。未接触前，接触区半宽为a；发生接触后，由于弹性变形，使接触区变宽，接触半宽变为b，接触区中心的黏着区半宽为c。
Ciavarella和Hills等针对该接触问题进行了深入研究，给出了该接触问题应力场分布的近似解。鉴于篇幅和内容所限，本书仅给出相关的结论，具体的求解和推导过程，读者可查阅相关文献。
在接触区-b＜x＜b内，令
x=bsinφ （2.41）
b=asinφ0 （2.42）
图2.6 带圆角的平面接触问题模型
则接触区的接触压力分布为
φ0可由下式确定：
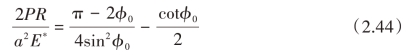
将接触压力做归一化处理，不同情况下的接触压力分布如图2.7所示。可见，面-面接触区的接触压力分布并不为均匀分布，距接触区边缘越近应力梯度越大。理论上讲，当a/b=1，即无圆角的理想协调接触状态下，接触区边缘的接触压力趋于无穷大。反之，当a/b=0时该问题退化为Hertz接触问题。
接触表面切应力的分布为
(www.xing528.com)
其中，R*由下式确定：
式中，R为接触面边缘的圆角。
图2.7 面-面接触情况接触表面的接触应力分布
黏着区半宽c可由下式确定：
将切应力做归一化处理，不同情况下，接触表面的切应力分布如图2.8所示。可见，接触区切应力分布的计算值与实际分布存在一定的误差，但总体趋势一致，结果较为合理。
图2.8 面-面接触情况接触表面的切应力分布
（a）a/b=0.3时不同载荷状态下的切应力分布
图2.8 面-面接触情况接触表面的切应力分布（续）
（b）a/b=0.8时不同载荷状态下的切应力分布
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
