【摘要】:进行微动疲劳试验时,试件除受到微动垫的法向载荷外,还受到远端交变载荷σB的作用。此时接触面上的应力分布将由于远端载荷的作用而发生变化。Nowell和Hills对该情况进行了分析,给出了此时接触面上应力分布的解析解。但是由于远端载荷的影响,接触区的中心会偏移一个小量e,即此时接触中心的坐标为x=e。根据几何约束条件可知e+c≤a,因此式(2.4)成立的条件为图2.5远端载荷作用下接触面切应力的分布
进行微动疲劳试验时,试件除受到微动垫的法向载荷外,还受到远端交变载荷σB的作用。此时接触面上的应力分布将由于远端载荷的作用而发生变化。Nowell和Hills对该情况进行了分析,给出了此时接触面上应力分布的解析解。
Nowell和Hills认为,当σB较小(σBa/Q→0)时,接触区的法向接触压力的分布满足Hertz给出的表达式,切应力分布与Mindlin给出的结果相似。但是由于远端载荷的影响,接触区的中心会偏移一个小量e,即此时接触中心的坐标为x=e。此时的接触应力场分布为
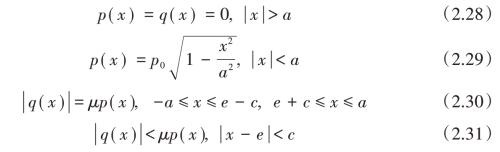
因为在黏着区无滑动,因此两弹性体接触区表面的应变应该相等,即
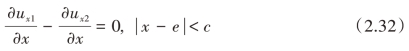
对于弹性接触体1(不受远端载荷作用),接触表面的应变为
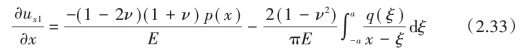
对于弹性接触体2(受远端载荷作用),接触表面的应变需要将远端载荷的作用考虑在内,即
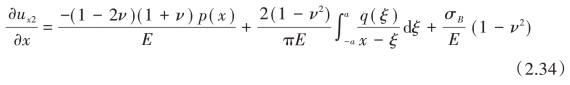
将式(2.34)和式(2.33)两式相减得
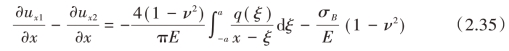
调用式(2.33)并将q(x)的表达式代入得(https://www.xing528.com)
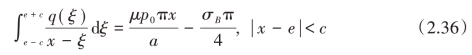
要使该等式成立,必须满足

以及
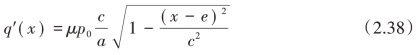
因此,最终的结果为
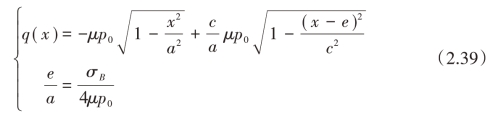
根据上述分析结果,典型的切应力场分布如图2.5所示。根据几何约束条件可知e+c≤a,因此式(2.4)成立的条件为
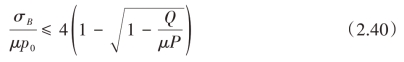
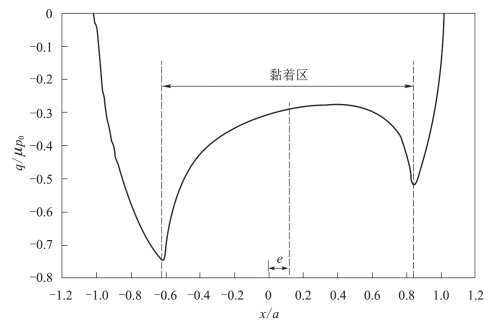
图2.5 远端载荷作用下接触面切应力的分布(Q/(μP)=0.5,σB/(μp0)=0.5)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




