微动疲劳是与接触相关的，对接触面的接触状态和应力-应变场分布的分析计算是微动疲劳损伤分析的关键。有限元法作为结构强度分析的有效工具，是微动疲劳损伤机理与疲劳寿命预测分析的重要手段。
接触是一种高度非线性的问题，其边界条件不能在计算开始时全部给出，边界条件在计算过程中不断变化，系统的刚度依赖于接触状态，因此需要计算过程中对节点间的状态进行不断搜索和判断，因此计算时需要较多的计算资源。其对于网格质量和接触参数设置要求较高，技巧性较强，如果参数设置不好，会导致计算难以收敛或计算结果误差较大。经过多年的发展，应用有限元法求解接触问题有了长足的发展，目前已有多种接触算法能够很好地解决接触问题。
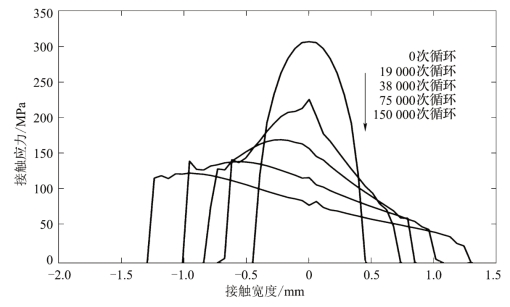
微动过程中的磨损会导致接触区的几何特性发生变化，进而引起接触应力场及接触状态的变化。反过来，接触应力场的变化又会导致微动区域磨损状态的改变。因此，微动过程中接触区应力场与微动磨损均为时变过程，两者存在明显的耦合关系。如图1.20所示，随着循环次数的增加，接触区会逐渐变大，接触区正应力峰值逐渐减小。因此，若要精确分析微动疲劳的演化过程，必须在有限元分析过程中考虑疲劳与磨损的相互作用关系，建立疲劳-磨损耦合求解的计算模型。由于微动损伤的复杂性和时变特性，目前大多数预测方法采用数值算法对磨损和疲劳损伤的演化过程进行迭代计算。McColl等考虑了磨损与应力场之间的耦合关系，采用有限元方法对微动磨损进行计算，仿真结果与试验吻合。Madge等在此基础上又将基于多轴疲劳的SWT准则应用于微动损伤的仿真分析，提出了磨损——裂纹萌生——裂纹扩展的分段计算模型，实现了磨损与疲劳损伤的耦合计算，使数值模拟更加精确。计算流程如图1.21所示，首先基于磨损Archard模型计算接触区各节点位置的磨损量，通过编写ABAQUS用户子程序对接触区几何进行更新并重新计算接触区应力-应变场分布；其次基于多轴疲劳临界面法的SWT模型计算各节点位置的疲劳损伤并应用Miner线性损伤累积理论对各节点的总损伤进行计算，进而判断微动疲劳的萌生位置；最后基于断裂力学理论对裂纹扩展行为进行计算。利用现代高性能计算机，此类算法已经可以实现对微动磨损和微动疲劳寿命的计算分析。然而，微动接触计算需要对网格进行较高程度的细化，而微动磨损的计算由于涉及材料磨掉后的构型改变，需要进行有限元网格的更新，计算成本较高，还需要开发高速、高性能的计算方法。
(www.xing528.com)
图1.20 考虑磨损的接触区接触应力场分布的有限元计算结果
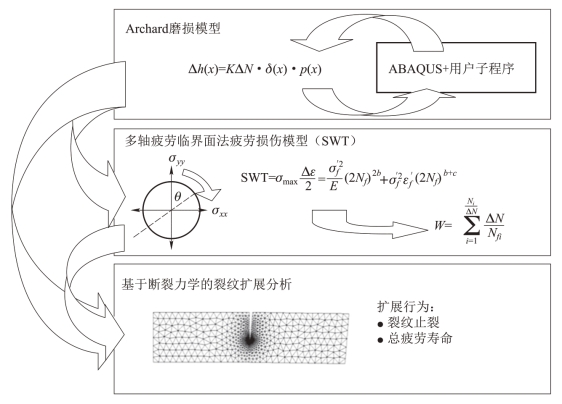
图1.21 磨损——裂纹萌生——裂纹扩展有限元模型的计算流程
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
