溶质再分配规律：固液共存条件下的溶质平衡分配系数对合金结晶过程的影响

（一）溶质的平衡分配系数

单相固溶体的合金结晶有两个结晶温度：结晶开始的温度和结晶完毕的温度。在平衡相图上前者即液相线温度T L，后者即固相线温度T S成分为C0的合金在T L至T S的结晶温度范围内的某一温度T进行结晶时，溶质在固相中的浓度为C S而溶质在液相中的浓度为C L（见图8-26），两者的比值为K 0，即：

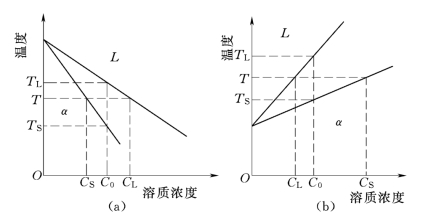
图8-26　K　0＜1及K　0＞I的两类二元相图

如果固相线和液相线都是直线（在溶质含量较低的范围内可以这样认为），不同温度下虽有不同的平衡浓度C S和C L，但其比值K 0恒为常数，它与溶液的浓度无关，只决定于溶剂和溶质的性质。K 0由平衡相图中直接求得，用以表征固、液两相共存的热力学平衡性质，故称为溶质平衡分配系数。K 0＜1，说明溶质元素降低固相线温度和液相线温度；K 0＞1，说明溶质元素提高固相线温度和液相线温度。

（二）平衡结晶时的溶质再分布

如果结晶过程极其缓慢，使溶质在固相和液相中得以充分扩散达到均匀化，就可以实现平衡结晶。

为研究方便，假设：有一棒状试样沿水平方向自左向右进行单向凝固；在结晶过程中固—液界面始终为平面；固相线和液相线都是直线，即K 0恒为常数；K 0＜1；合金熔液的原始成分为C0，如图8-27所示。

成分为C 0的合金在冷到T L以下便开始结晶，析出固相的浓度为K 0 C0（低于C0），多余的溶质原子从界面上排出来并充分扩散到液相中，使液相浓度稍高于C0，如图8-27（b）所示。在继续冷却和结晶过程中，固相不断增加而液相不断减少，固相和液相浓度分别按固相线和液相线变化。在温度T′时，界面处固相和液相浓度分别为C′S和C′L。由于溶质在固相和液相中的扩散是充分的，故全部固相浓度是均匀的（C S=C′S），整个液相浓度也是均匀的（C L=C′L），如图8-27（c）所示。依据杠杆定律，固相的重量分数f S和液相的重量分数f L之间存在如下关系：

图8-27　平衡结晶时的溶质再分布

（a）相图；（b）开始结晶时；（c）温度T′时；（d）结晶完毕时

式（8-21）称为平衡杠杆定律。结晶完毕时，全部固相浓度都变为C0。在实际生产中平衡结晶是难以达到的，平衡杠杆定律无法应用，只是作为必须了解的理论基础。

（三）非平衡结晶时的溶质再分布

实际生产中金属液结晶较快，溶质在液体和固体中都不可能充分扩散均匀，所以是非平衡结晶。对于所有的液态金属，原子扩散系数D L约为5×10-5 cm2/s数量级；而在结晶温度下，溶质在固相中的扩散系数D S约为10-8 cm2/s数量级。因此，在分析实际的结晶问题时往往忽略溶质在固相中的扩散，而仅考虑溶质在液相中的扩散以及由于液体对流或进行搅拌造成的溶质混合现象。非平衡结晶大致分为三种情况：①固相中无扩散，液相中均匀混合；②固相中无扩散，液相中只有扩散没有对流或搅拌；③固相中无扩散，液相中有扩散及对流。本教材只讨论前两种情况。

1.固相中无扩散、液相中均匀混合

这种情况与前面讨论的平衡结晶情况的唯一差别只是固相中无溶质扩散。讨论时仍假定：合金自左向右进行单向凝固，固—液界面始终为平面，K 0＜1，且恒为常数，合金原始成分为C 0。虽然整个系统是非平衡，但可假定在固—液界面上存在着局部平衡，即界面上的固相浓度C′S与液相浓度C′L由溶质平衡分配系数K 0决定。由于假定K 0恒为常数，故C′L变化时C′S应按C′S=K 0 C′L而相应变化。

图8-28示出固相中无扩散、液相中均匀混合情况下的溶质再分布。

开始结晶时析出的固相浓度为K 0 C0，液相浓度C′L≈C 0[见图8-28（b）]。温度继续下降时析出的固相的浓度随固相线而变；但由于各温度下析出的固相之间无溶质扩散，故在温度为T′时，已析出的固相中浓度不均匀，它由K 0 C 0逐渐变化到C′S而液相中的浓度则是均匀的，此时各处均为C′L，如图8-28（c）所示。显然，整个固相的平均浓度C S低于平衡结晶时的固相浓度C S；固相平均浓度线如图8-28（a）中虚线1—2所示。

根据溶质守恒，固相的重量分数f S与液相的重量分数f L之间存在如下关系：

图8-28　固相中无扩散、液相中均匀混合情况下的溶质再分布

（a）相图；（b）开始结晶时；（c）温度T′时；（d）温度T E时

在相同温度下，f S和C L保持不变，但C S＜C S，因而剩余液相的量f L比平衡结晶时增多。如果C0大于T E时的固相平均浓度[见图8-28（a）中虚线的2点]，则在T E时有共晶浓度C E的液体残留[见图8-28（d）]下来，最后转变为共晶组织。

在这种条件下结晶的固体，其浓度极不均匀。这种成分不均匀性产生于晶粒内部称为晶内偏析。对于上述单向凝固的柱形棒，从棒的一端到另一端产生显著的成分差异，也可以称为宏观偏析。这种偏析的定量规律可用非平衡杠杆定律描述：

(www.xing528.com)

式（8-23）称为非平衡杠杆定律，或称夏尔方程。

可知，固体棒凝固后得到的溶质分布曲线是随K 0值而变。图8-29是不同K 0时的溶质分布曲线。可见，在K 0＜l时，如果柱形棒从左向右进行液相均匀混合条件下的单向凝固，则左端获得纯化，溶质富集于右端。

2.固相中无扩散、液相中只有扩散而无对流或搅拌

讨论时除保留前述假定外还假定试样足够长。这种情况下的溶质再分布如图8-30所示。

合金自左端冷到稍低于T L时便开始结晶，析出的固相浓度为K 0C0，排出的溶质集中在固—液界面上并按扩散规律在固—液界面前沿液相中分布[见图8-30（b）]。由于试样足够长，远处液相浓度仍为C 0。界面前沿液相中溶质的富集，使界面处液相结晶的开始温度下降；只有在界面处溶质富集程度减少且温度进一步下降时，界面才能生长。当界面温度降至T′时，界面处固相浓度为C S′而液相浓度为C′L[见图8-30（c）]。当界面温度下降达到T S时，界面处固相浓度为C0，而液相浓度为C0/K 0[见图8 30（d）]。

单位时间内单位面积界面上排出的溶质，即质流密度q1：

图8-29　固相中无扩散、液相中均匀混合时柱形棒凝固后的溶质分布曲线

式中 R——晶体生长速度，即界面向液体中的推进速度。

界面处溶质向液体中扩散的质流密度q2决定于扩散第一定律：

当界面向液相推进时，界面前沿液相中溶质富集程度增加，相应地q2便增大；当q2加大到一定程度时，q2=q1，于是达到稳定生长阶段。从结晶开始到建立稳定生长为止的这一段称为初始过渡区[见图8-30（g）]，此区特点是q1＞q2。

图8-30　固相中无扩散，液相中只有扩散而无对流（K　0＜1）情况下的溶质再分布

（a）相图；（b）开始结晶；（c）温度T′时；（d）界面温度达T S时；（e）稳定生长过程中；（f）结晶完毕时；（g）结晶过程中固相与液相浓度变化

在稳定生长阶段，由于q1=q2，结晶接近完毕时，界面处富集的溶质已无处可扩散，全部集中在残余液相中，使液相浓度大为增高；最后，结晶完毕时试样终端的溶质浓度C S很高[见图8-30（f）、（g）]。

稳定生长阶段界面前沿液相中存在溶质富集层这一现象对结晶过程影响很大，溶质富集层中溶质分布的规律界面前沿液相中溶质分布曲线示意于图8-31。

图8-31　稳定生长阶段界面前沿液相中溶质分布曲线

（a）K 0＜1；（b）K 0＞1

稳定生长阶段固—液界面前沿液相中的溶质浓度分市曲线的数学表达式为：

当K 0＜1，它是一条指数衰减曲线[见图8-31（a）]，表明：随着x的增加，液相中溶质浓度按指数规律减小并趋于C0。

对于K 0＞1的单相合金，在稳定生长阶段固—液界面前沿液相中的溶质浓度分布曲线的数学表达式与式（8-26），相同，但曲线被颠倒过来[见图8-31（b）]。

由式（8-26）可知，溶质浓度分布曲线的形状受R、D L和K 0三个因素的影响，如图8-32所示。可见，当R高或D L小时，就会产生一段短而陡的溶质富集层。当K 0很小时，界面前沿液相中会出现严重的溶质富集。

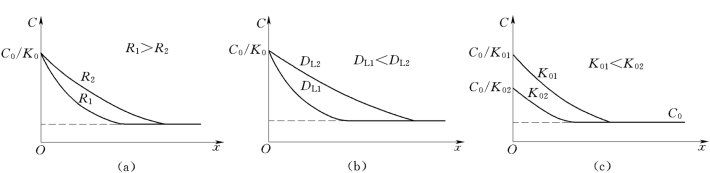
图8-32　R、D　L、K　0对界面前沿液相中溶质浓度分布曲线的影响（K　0＜1）

以上讨论非平衡结晶时都假定在固—液界面上存在着局部平衡，即界面上的固相浓度与液相浓度由溶质平衡分配系数K 0决定，但实际情况并非如此。试验研究指出，对于K 0＜1的合金，在非平衡结晶条件下，固—液界面上固相浓度与液相浓度之比（即溶质实际分配系数K）大于K 0，而且K对K 0的偏离（用K/K 0表示）随冷却速度的增大而加大；在温度固定不变的条件下，界面上固相浓度和液相浓度都随着保温时间的延续而不断下降，且其比值K也随之下降（即K对K 0的偏离随之减小）；当保温时间足够长时，K对K 0的偏离几乎为零，即K趋近于K 0。