金属自发形核的临界过冷度及规律分析

根据液态金属结构的现代理论，在铸造的温度条件下，液态金属中的原子呈近程有序排列，即从大范围来看，原子排列是不规则的，但从局部微观区域来看，原子可以偶尔在某一瞬间内出现规则的排列，然后又散开，这种瞬间内存在的微观区域内的规则排列称为“近程有序”。这种近程有序排列的原子集团处于瞬息变化状态：时而长大，时而变小，时而产生，时而消失，此起彼落。这种近程有序排列的原子集团就是晶胚；在具备一定条件后，大于某一定尺寸的晶胚就会成为晶核。

（一）自发形核时能量的变化

过冷的液态金属中出现晶胚时，一部分原子从液态的聚集状态转变为固态的排列状态，处于晶胚内部，引起体系体积自由能的降低；另一部分原子构成晶胚的表面，引起体系表面自由能的增加。当过冷液态金属中形成一个半径为r的球形晶胚时，其总的自由能变化ΔG应为：

式中 ΔGⅤ——单位体积自由能的变化；

σLC——晶胚与液态金属之间的单位表面自由能（或称界面张力）。

在一定温度下，ΔGⅤ和的数值是确定的，因此，ΔG是r的函数。ΔG随r的变化可用图8-4来表示。

图8-4　ΔG随r的变化曲线示意图

与ΔG*0对应的晶胚半径为r*。凡是半径小于r*的晶胚，都不可能长大（因为晶胚长大将使ΔG增大，这在热力学上是不可能的）；相反，它只会自发地减小以至消失。只有半径大于r*的晶胚，才能自发地长大（因为长大过程中，ΔG将减小）。半径为r*的晶胚是不稳定的，如果它获得一个原子便会自发长大；如果它失去一个原子便会自发减小以至消失。r*是一个临界值，称为临界半径。半径等于r*的晶胚称为临界晶核，半径大于r*的晶胚称为晶核。

将式（8-1）对r求导，并使之等于零，则可求得临界半径为：

式中 L——金属的结晶潜热；

T m——金属的熔点。

对于既定的金属，T m和L都是常数，而σLC可近似地认为不随温度变化。因此，ΔG*与ΔT的平方成反比，它说明临界晶核形核功随过冷度的增加而显著减小。

图8-5　自发形核临界过冷度示意图(www.xing528.com)

1—晶核临界半径r*和过冷度ΔT的关系；2—最大晶胚尺寸r max与过冷度ΔT之间的关系

从式（8-1）、式（8-4）及式（8-5）可以看出，临界晶核形核功等于临界晶核界面能的1/3。这表明，形成临界晶核时，体积能的减小只能补偿2/3的界面能，还缺1/3的界面能必须由液相中局部的能量起伏来提供。当液相中的某一微观区域内出现达到形成临界晶核所需的能量起伏时，在此区域内就可能形成晶核。

综上所述，在过冷的液态金属中，当某一微观区域内同时出现大于临界半径的相起伏和等于临界晶核形核功的能量起伏时，一个晶核便在该区域形成。

液相中最大晶胚尺寸r max与过冷度ΔT之间存在图8-5中曲线2所示关系。

两曲线的交点N所对应的过冷度ΔT*称为自发形核临界过冷度。在ΔT*时，所对应的最大晶胚尺寸即为临界晶核半径r*。当ΔT＜ΔT*时，r max＜r*，晶胚不能成为晶核。当ΔT＞ΔT*时，r max＞r*，液相中将出现自发形核。

实验指出，对于许多金属而言，自发形核所需过冷度约为0.18～0.20T m。

（二）自发形核的形核率

形核率Ⅰ定义为单位时间内于单位体积液体中形成的晶核数。

在过冷液体中自发形核需要同时出现：达到ΔG*的能量起伏和大于r*的相起伏。能量起伏达到ΔG*的几率应与几率因子exp（-ΔG*/k T）成正比，临界尺寸的晶胚要变为晶核，需要由其周围的液体中至少补充一个原子，也就是需要原子由液相跨越界面跳动到晶胚上。设原子由液相跨越界面跳到晶胚所需的激活能为ΔG A，则由临界尺寸的晶胚变为晶核的几率应与几率因子exp（-ΔG A/k T）成正比。因此，自发形核率I*应与上述两个几率因子成正比，其表达式为：

式中 k——玻尔茨曼常数，k=1.38×10-23 J/K；

T——温度；

KⅤ——比例常数。

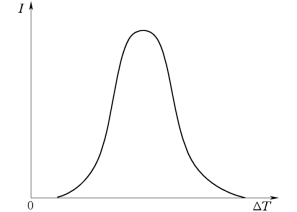
图8-6　自发形核率随过冷度变化的理论关系

由式（8-5）可知，ΔG*与过冷度ΔT（ΔT=T m-T）的平方成反比，因此当ΔT很小并趋于零时，ΔG*趋于无限大，exp（-ΔG*/k T）则趋于零。过冷度增大则exp（-ΔG*/k T）也增大。ΔG A与温度或过冷度的关系不大，可视为常数。因此exp（-ΔG A/k T）随ΔT的增大而减小；当ΔT很大时，exp（-ΔG A/k T）变得很小。这两个相互矛盾因素的综合结果，使自发形核率随过冷度的变化曲线出现一个极大值，如图8-6所示。

图8-6所示关系适用于玻璃及高分子化合物之类的高粘性液体。但对液态金属，由于原子活动能力强，不易出现极大值，即看不到形核率随过冷度增大而减小的部分，如图8-7所示。所以，对金属而言，在一般铸造的冷却条件下，其形核率随过冷度增大而增大。

以上讨论的是纯金属的自发形核，其液体只由同种原子组成，其晶胚及晶核的成分与液体相同。对于合金而言，情况就复杂多了。由于固体晶核与不同成分的液体之间要维持平衡所以在形核过程中，扩散将起很大作用。