铸件的凝固时间,是指从液态金属充满型腔后至凝固完毕所需的时间。
铸件的凝固时间可以用热电偶直接测定,也可以通过计算来确定。在分析铸件与铸型之间热交换特点时已经提到有四种情况,现介绍最常用的砂型铸造(即铸型热阻起决定性作用)(图7-4)情况下的铸件凝固时间计算。
为使问题简化,假设:①铸件和铸型都是半无限大,其接触界面为无限大平面;②与液态金属接触的铸型表面温度,浇注后立即升到铸件表面温度,且以后保持不变;③凝固是在恒温下进行的;④除凝固潜热外,在凝固过程中没有释放其他热量;⑤铸型和金属的热物理性质不随温度而变化;⑥由于液态金属对流作用引起的温度场改变,可以忽略不计;⑦与凝固潜热相比,金属的显热(即从浇注温度至熔点之间放出的过热热量)可以忽略不计。
根据上述假设,铸件凝固过程某一瞬间铸件及铸型断面上的温度分布见图7-4(a),并令凝固层厚度为ξ:
![]()
式(7-7)称为“平方根定律”,即凝固层厚度与时间的平方根成正比。式中K称为铸件的凝固系数,其值可用实验方法求得(见表7-4)。
表7-4 几种合金在砂型中的凝固系数K

令平板铸件厚度为T,当凝固层厚度达T/2时,铸件就凝固完毕,所需时间即凝固时间τ:
![]()
式(7-8)表明,平板铸件的凝固时间与铸件厚度的平方成正比。
对于平板以外形状(如圆柱体、方柱体、球等)的铸件,可用铸件体积(V)与铸件表面积(A)的比值(V/A)来代替平板厚度。因为平板铸件的V/A比值为平板厚度的一半,故式(7-8)改写为:

式中 M——铸件凝固模数,简称模数,又称当量厚度、引用厚度等。
式(7-9)即著名的“Chvorinov”法则或公式。(https://www.xing528.com)
将式(7-9)取对数,并令K为定值,则在双对数坐标图中,τ与M成直线关系。图7-21是各种形状的钢铸件(重量从10kg到65t)的实测凝固时间与模数的关系。
由图7-21可以看出,所有的点都位于直线附近,表明无论铸件的重量如何,只要它们的模数相等,其凝固时间就相等或相近。
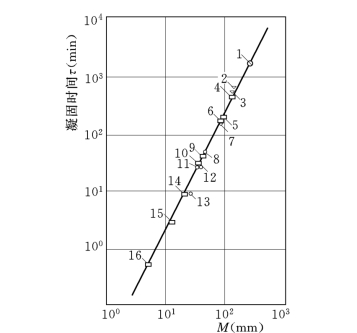
图7-21 钢铸件的凝固时间与模数的关系(单位:mm)
1—底座(重65t);2—环形冒口;3—环形铸件;4—平板(350×1800×2400);5—平板(200×1800×2400);6—平板(200×1500×1800);7—圆柱(Φ400×800);8—圆柱(Φ200×800);9—平板(100×800×800);10—平板(100×400×400);11—圆柱(Φ150×800);12—球(Φ229);13—球(Φ153);14—平板(50×400×400);15—平板(30×400×400);16—平板(10×400×400)
由于式(7-9)是在假定铸件与铸型接触面为平面的条件下(即热流相互平行地从铸件表面流出这一前提下)推导出来的,所以它用于计算大平板的凝固时间比较准确。对于短杆、立方体、圆柱体和球体形铸件,计算结果一般要比实际凝固时间长10%~15%。从图7-21中已经看到这种现象,例如200mm×1500mm×1800mm的平板与Φ400mm×800mm的圆柱体,它们的模数相等,但圆柱体的凝固时间短于平板。
由于圆柱体和球形铸件的表面为凸面,从铸件向铸型散出的热流不是相互平行的,而是以圆柱体的中心轴或球体的球心按放射状向外散热。凝固前沿的表面积在整个凝固期间不断地缩小,而型壁的表面积则为铸件尺寸所决定,为一定值。因此,凝固前沿向内推进的速度(dξ/dτ)就逐渐加快,当凝固前沿快抵达铸件中心时,由于凝固前沿表面积趋于零,此时(dξ/dτ)将变至无穷大。此外,与铸件凸面对应的铸型型壁是凹形的(见图7-22);铸件与铸型的接触表面积虽相同(1cm2),但对比型壁厚度δ相同的砂层,可以看出,圆柱体及球形情况比平面拥有更多的砂量。因而,在模数相同的条件下,球体凝固快于圆柱体,而圆柱体凝固快于平板。
图7-23是模数相同(M=1cm)而形状不同的球体、圆柱体、平板的可锻铸铁白口坯件的冷却曲线。可以看出,球形铸件比圆柱体铸件凝固快,圆柱体铸件比平板铸件凝固快。
Chworinov法则虽然并不很准确,但是在不需要精确计算时,却是最有用的近似计算法则。

图7-22 在接触面积和砂层厚度都相同条件下砂层量的对比
(a)平面型壁;(b)凹面型壁

图7-23 可锻铸铁白口坯件的冷却曲线(模数相同而形状不同)
1—球;2—圆柱体;3—平板
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




